Alternate solution II, January 18, 2007

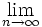
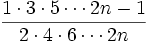
Find the limit $\lim_{n\rightarrow \infty}$ $\frac{1\cdot 3 \cdot 5 \cdots 2n-1}{2\cdot 4 \cdot 6 \cdots 2n}$

Kit remarked that the product is reminiscent of the famous Wallis product. (http://en.wikipedia.org/wiki/Wallis_product) landen took the product and made a new proof.

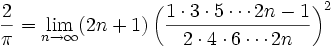
$\frac{2}{\pi} = \lim_{n\rightarrow \infty} (2n+1)\left(\frac{1\cdot 3 \cdot 5 \cdots 2n-1}{2\cdot 4 \cdot 6 \cdots 2n}\right)^2$

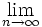
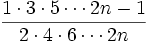
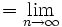
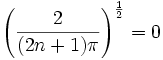
$\lim_{n\rightarrow \infty}$ $\frac{1\cdot 3 \cdot 5 \cdots 2n-1}{2\cdot 4 \cdot 6 \cdots 2n}$ $=\lim_{n\rightarrow \infty}$ $\left(\frac{2}{(2n+1)\pi}\right)^\frac{1}{2} = 0$

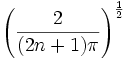$\left(\frac{2}{(2n+1)\pi}\right)^\frac{1}{2}$ is also a decent approximation to the finite products. $\qquad\square$

Retrieved from "http://www.efnet-math.org/w/Alternate_solution_II%2C_January_18%2C_2007"