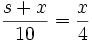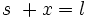Math Related Rates

Question Formulation

A classic related rates question is usually asked in #math by first year calculus students:

A street light is at the top of a 10 ft tall pole. A woman 6 ft tall walks away from the pole with a speed of 6 ft/sec along a straight path. How fast is the tip of her shadow moving when she is 40 ft from the base of the pole?

Answer

The first step that should be taken is to make a diagram from which we can model an equation or equations that relates the variables of the problem.

Let the woman's distance from the pole be x, the length of the shadow s, the distance from the tip of the shadow to the base of the pole be l.

Now, going back to the word problem, we see that we're asked for the rate at which the tip of the shadow is moving.

A common mistake is to attempt to solve for ds / dt. However, notice that the rate at which the tip of the shadow is moving is equivalent to the rate at which the total distance from the tip of the shadow to the base of the pole is growing ... in other words, dl / dt needs to be solved for -- this is fundamentally different from attempting to solve for rate at which the shadow's length is increasing.

By noting the similar triangles in the diagram, we can setup an equation such as the one below:

Since

l/10 = x/4

 l = (5 / 2)x

Now we can differentiate.

dl / dt = (5 / 2) dx / dt

The rate at which the woman is walking is constant. dx / dt = 6 ft / s

Therefore, dl / dt = (5 / 2) * 6 ft / s = 15 ft / s, regardless of her distance from the pole.