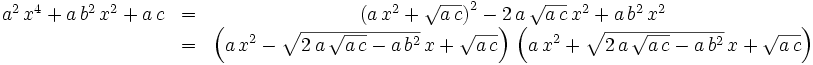Quartics

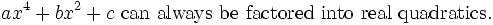
$ax^4 + bx^2 + c\mbox{ can always be factored into real quadratics.}\,$

by landen

After it is factored, you can easily solve it by using the quadratic formula on the two real factors. Or you can use the factors for solving partial fraction integrals. We can take $a > 0$ and also multiply by $4 a$ to avoid fractions.

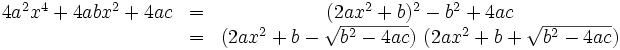
Suppose $b 2 - 4 a c$ > 0 $\begin{matrix} 4a^2x^4 + 4abx^2 + 4ac &= &(2ax^2 + b)^2 -b^2 + 4ac\\ &= &(2ax^2+b - \sqrt{b^2-4ac})\ (2ax^2+b + \sqrt{b^2-4ac}) \end{matrix}$

Suppose $b 2 - 4 a c < 0$ then $4 a c > 0$ $\begin{matrix} a^2\,x^4+a\,b^2\,x^2+a\,c&=&\left(a\,x^2+\sqrt{a\,c}\right)^2-2\,a\,\sqrt{a\,c}\,x^2+a\,b^2\,x^2\\ &=&\left(a\,x^2-\sqrt{2\,a\,\sqrt{a\,c}-a\,b^2}\,x+\sqrt{a\,c}\right) \,\left(a\,x^2+\sqrt{2\,a\,\sqrt{a\,c}-a\,b^2}\,x+\sqrt{a\,c}\right) \end{matrix}$

Retrieved from "http://www.efnet-math.org/w/Quartics"