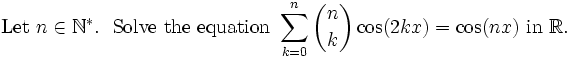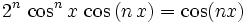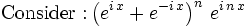Sol032106

$\mathrm{Let\ }n\in\mathbb{N}^* .\mathrm{\ \ Solve\ the\ equation\ }\sum_{k=0}^n {n \choose k}\cos(2kx)=\cos (nx)\mathrm{\ in\ }\mathbb{R}.\,$

Solution by landen

The left side of the problem can be summed(method below) in closed form to get:

$\sum_{k=0}^n {n\choose k}\cos(2kx)=2^{n}\,\cos ^{n}x\,\cos \left(n\,x\right)$

Now we can solve:

$2^{n}\,\cos ^{n}x\,\cos \left(n\,x\right)=\cos (nx)$

We get a pile of solutions when $n x$ is an odd multiple of $π / 2$ , because $cos(n x) = 0$ . When $cos(n x)$ is non-zero, we can divide it out to get:

$\cos ^{n}x = 1/2^n\,$

This provides an infinite set of solutions when $cos(x) = 1 / 2$ . If n is even there is another set when $cos(x) = - 1 / 2$ .

The trig identity justification

$\mathrm{Consider: }\left(e^{i\,x}+e^ {- i\,x }\right)^{n}\,e^{i\,n\,x}$

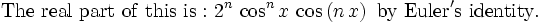
$\mathrm{The\ real\ part\ of\ this\ is:\ }2^{n}\,\cos ^{n}x\,\cos \left(n\,x\right)\mathrm{\ by\ Euler's\ identity.}$

We can expand with the binary formula first, use Euler's identity, take the real part, and get exactly the sum we need so:

$\sum_{k=0}^n {n \choose k}\cos(2kx)=2^{n}\,\cos ^{n}x\,\cos \left(n\,x\right)$

$\square$

Retrieved from "http://www.efnet-math.org/w/Sol032106"