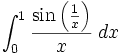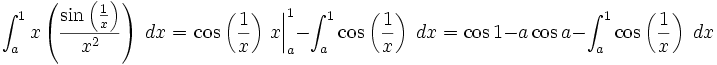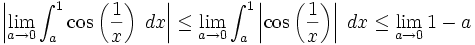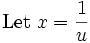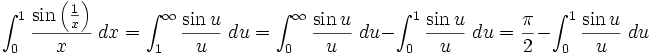Sol032406

from landen

Show this integral converges:

$\int_{0}^{1}{{{\sin \left({{1}\over{x}}\right)}\over{x}}\;dx}$

Proof from landen

For a>0 , rewrite it, and integrate by parts:

$\int_{a}^{1}{x\left({{\sin \left({{1}\over{x}}\right)}\over{x^2}} \right)\;dx} = \left.\cos \left({{1}\over{x}}\right)\,x\right |_a^1-\int_{a}^{1}{\cos \left({{1}\over{x}}\right)\;dx}=\cos 1-a\cos a-\int_{a}^{1}{\cos \left({{1}\over{x}}\right)\;dx}$

Notice that:

$\left| \lim_{a\rightarrow 0}{\int_{a}^{1}{\cos \left({{1}\over{x}} \right)\;dx}}\right| \le\lim_{a\rightarrow 0}{\int_{a}^{1}{\left| \cos \left({{1}\over{x}} \right)\right| \;dx}}\le \lim_{a\rightarrow 0}{1-a}$

The limits as 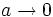$a\rightarrow 0$ exist and establish that the integral converges. $\square$

Can you get a numerical approximation of the value to a bunch of decimal places?

Karlsen and dioid used Mathematica and Maple and both packages could get many decimal places almost instantly. landen used a homebrew algorithm:

$\mathrm{Let\ }x={{1}\over{u}}$

$\int_{0}^{1}{{{\sin \left({{1}\over{x}}\right)}\over{x}}\;dx}= \int_{1}^{\infty }{{{\sin u}\over{u}}\;du}= \int_{0}^{\infty }{{{\sin u}\over{u}}\;du} -\int_{0}^{1}{{{\sin u}\over{u}}\;du}= {{\pi}\over{2}}-\int_{0}^{1}{{{\sin u}\over{u}}\;du}$

The $π / 2$ value for the infinite integral is a famous result. The remaining integral is easily integrated with Taylor's theorem and you can get an error term.

Everybody got approximately: 0.62471325642771360428996837781657178428624674494944 $\cdots$

Karlsen got 10000 digits!

Retrieved from "http://www.efnet-math.org/w/Sol032406"