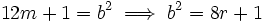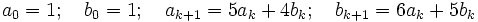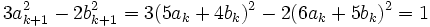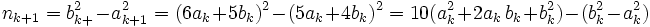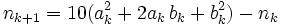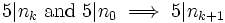Sol032506

If $2 n + 1$ and $3 n + 1$ are squares, $n$ is divisible by 40.

Solution by landen:

Let 2 n + 1 = a 2 and 3 n + 1 = b 2, then n = b 2 - a 2

Since $a$ is odd, $a 2 = 8 k + 1$ for some $k$ , by a famous result.

$2n+1=a^2=8k+1 \implies n=4m$

$12m+1=b^2 \implies b^2 = 8r+1$

$b^2-a^2 = n = 8(r-k)\,$

Now all we have left to show is that $5 | n$ ; After some manipulation and numbering solutions with k, we get:

$3a_k^2-2b_k^2=1; \qquad n_k=b_k^2-a_k^2\,$

There are infinitely many solutions given by a lucky guess linear recurrence:

$a_0=1;\quad b_0=1;\quad a_{k+1}=5a_k+4b_k;\quad b_{k+1}=6a_k+5b_k$

$3a_{k+1}^2-2b_{k+1}^2 = 3(5a_k+4b_k)^2 - 2(6a_k+5b_k)^2 = 1$

By induction, and assuming the $k$ case is true:

$n_{k+1}=b_{k+}^2-a_{k+1}^2=(6a_k+5b_k)^2-(5a_k+4b_k)^2=10(a_k^2+2a_k\,b_k+b_k^2) - (b_k^2-a_k^2)$

$n_{k+1}=10(a_k^2+2a_k\,b_k+b_k^2) - n_k$

$5|n_k \mbox{ and }5|n_0 \implies 5|n_{k+1}$

Now we have infinitely many solutions which are divisible by 40. But we need to know that $n k$ as defined above gives all solutions. This is done via the same argument used in HS Math Meet Quadratic Form Problem (http://efnet-math.org/math_tech/HyperQuadForm.html). The same reference shows a way to guess the linear recurrence by high school means. landen cheated and got Pari/GP, a powerful number theory package, to do the guessing.

Example:

$n\,$ =21977864161847389892411934700781467291095784894131460408800640

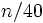$n/40\,$ = 549446604046184747310298367519536682277394622353286510220016

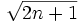$\sqrt{2n+1}$ = a = 6629911637698859994122683667841

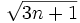$\sqrt{3n+1}$ = b =8119950276051089814163364091839

Retrieved from "http://www.efnet-math.org/w/Sol032506"