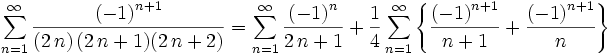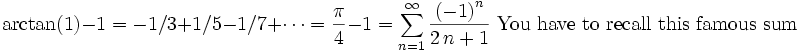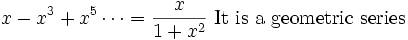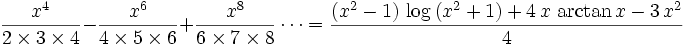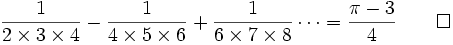Sol032606

from Anil

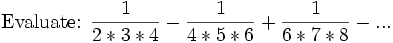
$\mbox{Evaluate: }\frac{1}{2*3*4} - \frac{1}{4*5*6} + \frac{1}{6*7*8} - ...$

Solution from Bump as told to landen

Using partial fractions on the general form of the sum:

$\sum_{n=1}^{\infty }{{{\left(-1\right)^{n+1}}\over{\left(2\,n \right)(2\,n+1)(2\,n+2)}}}= \sum_{n=1}^{\infty }{{{\left(-1\right)^{n}}\over{2\,n+1}}}+\frac{1}{4} \sum_{n=1}^{\infty }\left\{{{\left(-1\right)^{n+1}}\over{n+1}}+{{\left(-1\right)^{n+1} }\over{n}}\right\}$

$\arctan(1)-1=-1/3+1/5-1/7+\cdots=\frac{\pi}{4}-1=\sum_{n=1}^{\infty }{{{\left(-1\right)^{n}}\over{2\,n+1}}}\mbox{ You have to recall this famous sum}$

$\frac{1}{4} \lim_{m\rightarrow\infty}\sum_{n=1}^{m }\left\{{{\left(-1\right)^{n+1}}\over{n+1}}+{{\left(-1\right)^{n+1} }\over{n}}\right\}=\frac{1}{4}\left(1+\frac{(-1)^{m+1}}{m+1}\right)=\frac{1}{4}\mbox{ All the middle terms of the sum cancel}$

$\sum_{n=1}^{\infty }{{{\left(-1\right)^{n+1}}\over{\left(2\,n \right)(2\,n+1)(2\,n+2)}}}=\frac{\pi-3}{4}\mbox{ after combining the results}\qquad\square$

Solution from landen

One way to get consecutive integers in a denominator is to repeatedly integrate a power of x. Each integration puts another integer in the denominator.

$x-x^3+x^5\cdots = \frac{x}{1+x^2}\mbox{ It is a geometric series }$

Now we integrate both sides three times from 0 to $x$ :

$\frac{x^4}{2\times 3\times 4}-\frac{x^6}{4\times 5\times 6}+\frac{x^8}{6\times 7\times 8}\cdots ={{\left(x^2-1\right)\,\log \left(x^2+1\right)+4\,x\,\arctan x-3\,x^ 2}\over{4}}$

Next let $x$ =1:

$\frac{1}{2\times 3\times 4}-\frac{1}{4\times 5\times 6}+\frac{1}{6\times 7\times 8}\cdots =\frac{\pi-3}{4} \qquad\square$

Retrieved from "http://www.efnet-math.org/w/Sol032606"