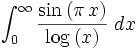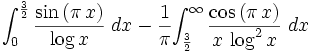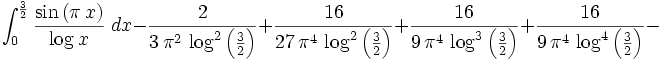Sol032906

Evaluate numerically with error bounds to a bunch of decimals if you can:

$\int_{0}^{\infty }{{{\sin \left(\pi\,x\right)}\over{\log\left(x \right)}}\;dx}$

Solution Theory by landen

This integrand has only limits at 0,1, and 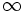$\infty$ . If your numerical integration program has problems you can split it into 3 parts and take limits at the singularity. If the routine doesn't happen to use exactly 0 or 1 for a point you can ignore the removable singularities at x=0 and 1. We can split the integration at 3/2 and then integrate the second integral by parts:

$\int_{0}^{{{3}\over{2}}}{{{\sin \left(\pi\,x\right)}\over{\log x}}\;dx}-\frac{1}{\pi}{{\int_{{{3}\over{2}}}^{\infty }{{{\cos \left(\pi\,x\right)}\over{ x\,\log ^2x}}\;dx}}}$

Notice that the integrals now converge absolutely and converge a little faster than the original. We can improve things by integrating by parts 5 times.

$\int_{0}^{{{3}\over{2}}}{{{\sin \left(\pi\,x\right)}\over{\log x}}\;dx}-{{2}\over{3\,\pi^2\,\log ^2\left({{3}\over{2}}\right)}}+{{16 }\over{27\,\pi^4\,\log ^2\left({{3}\over{2}}\right)}}+{{16}\over{9\, \pi^4\,\log ^3\left({{3}\over{2}}\right)}}+{{16}\over{9\,\pi^4\, \log ^4\left({{3}\over{2}}\right)}}-$

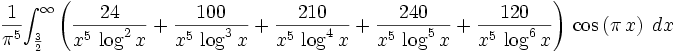
$\frac{1}{\pi^5}{{\int_{{{3}\over{2}}}^{\infty }{\left({{24}\over{x^5\,\log ^2x}}+ {{100}\over{x^5\,\log ^3x}}+{{210}\over{x^5\,\log ^4x}}+{{240}\over{ x^5\,\log ^5x}}+{{120}\over{x^5\,\log ^6x}}\right)\,\cos \left(\pi\, x\right)\;dx}}}$

The plan now is to do the integral to 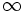$\infty$ as a sum of terms which are little integrals with limits that differ by 1

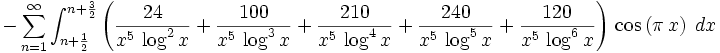
$-\sum_{n=1}^{\infty}{{{\int_{n+{{1}\over{2}}}^{n+{{3}\over{2}}}{\left({{24}\over{x^5\, \log ^2x}}+{{100}\over{x^5\,\log ^3x}}+{{210}\over{x^5\,\log ^4x}}+ {{240}\over{x^5\,\log ^5x}}+{{120}\over{x^5\,\log ^6x}}\right)\, \cos \left(\pi\,x\right)\;dx}}}}$

landen did the integrations by parts with a Maxima program and evaluated the numbers with Pari. The sum is alternating and decreasing monotonically so it gives an automatic error bracket. Below is the Pari program. Notice the sum is done backward which minimizes roundoff error. It was done using 19 digit arithmetic but showing only 14 digits. 80 terms gave this interval for the integral:
[-3.2191900386437, -3.2191900386455]

copy below into a file and \r filename into Pari, set floating precision with \p, etc.

integrand(x)=
{
local(u,ans);
u=log(x);
ans=-(1/x^5)*(24/(u^2)+100/(u^3)+210/(u^4)
+240/(u^5)+120/(u^6)) 
*cos(Pi*x) 
/Pi^5; 
return(ans); 
} 

term(n)= 
{ 
return(intnum(x=n+1/2,n+3/2,integrand(x))); 
} 

integral(m)= 
{ 
local(s); 
s=0; 
s+=sum(k=1,m,term(m+1-k)); 
s+=intnum(x=0,1,sin(Pi*x)/log(x),3); 
s+=intnum(x=1,3/2,sin(Pi*x)/log(x),3); 
s+=-2/(3*Pi^2*log(3/2)^2)+16/(27*Pi^4*log(3/2)^2) 
+16/(9*Pi^4*log(3/2)^3)+16/(9*Pi^4*log(3/2)^4); 
return([s,s+term(m+1)]); 
}

Retrieved from "http://www.efnet-math.org/w/Sol032906"