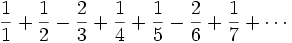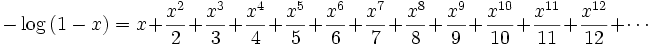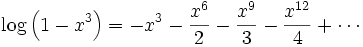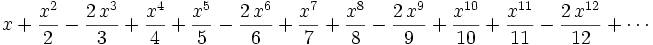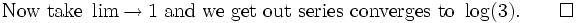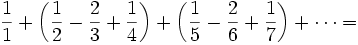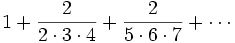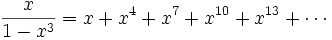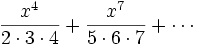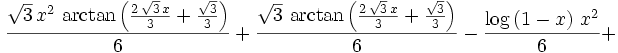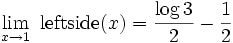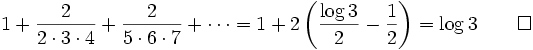Sol041406

from landen

Prove that the series

$\frac{1}{1}+\frac{1}{2}-\frac{2}{3}+\frac{1}{4}+\frac{1}{5}- \frac{2}{6}+\frac{1}{7}+\cdots$

converges and find its limit.

Solution I

We can regroup the series:

$\frac{1}{1}+\left(\frac{1}{2}-\frac{1}{3}\right)- \left(\frac{1}{3}-\frac{1}{4}\right)+ \left(\frac{1}{5}-\frac{1}{6}\right)-\left(\frac{1}{6}-\frac{1}{7}\right)+ \cdots$

The series now obviously converges conditionally by the alternating series test (http://pirate.shu.edu/projects/reals/numser/tests.html).

We recall that we can get increasing integers in denominators from properties of the $log$ function:

$-\log \left(1-x\right)=x+{{x^2}\over{2}}+{{x^3}\over{3}}+{{x^4 }\over{4}}+{{x^5}\over{5}}+{{x^6}\over{6}}+{{x^7}\over{7}}+{{x^8 }\over{8}}+{{x^9}\over{9}}+{{x^{10}}\over{10}}+{{x^{11}}\over{11}}+ {{x^{12}}\over{12}}+\cdots$

This is promising but the numerators are wrong for terms that are powers of $x 3$ . We can make another Taylor series with just these terms in it.

$\log \left(1-x^3\right)=-x^3-{{x^6}\over{2}}-{{x^9}\over{3}}-{{x^{ 12}}\over{4}}+\cdots$

Now add the two series and simplify.

$\log \left(1-x^3\right)-\log \left(1-x\right)=\log \left(x^2+x+1 \right)=$

$x+{{x^2}\over{2}}-{{2\,x^3}\over{3}}+{{x^4}\over{4}}+{{x^5}\over{5 }}-{{2\,x^6}\over{6}}+{{x^7}\over{7}}+{{x^8}\over{8}}-{{2\,x^9}\over{9 }}+{{x^{10}}\over{10}}+{{x^{11}}\over{11}}-{{2\,x^{12}}\over{12}} +\cdots$

$\mbox{Now take }\lim{\rightarrow 1}\mbox{ and we get out series converges to }\log(3).\qquad \square$

Solution II

$\frac{1}{1}+\left(\frac{1}{2}-\frac{2}{3}+\frac{1}{4}\right)+\left(\frac{1}{5}- \frac{2}{6}+\frac{1}{7}\right)+\cdots =$

$1 + \frac{2}{2\cdot 3 \cdot 4} + \frac{2}{5\cdot 6\cdot 7} +\cdots$

Which now converges absolutely. This solution follows the idea of landen's solution to the March 26, 2006 problem from Anil. Consider the geometric series:

$\frac{x}{1-x^3} = x+x^4 + x^7 + x^{10}+x^{13}+\cdots$

If we integrate both sides, three times from 0 to $x$ , on the right we get:

$\frac{x^4}{2\cdot 3 \cdot 4} + \frac{x^7}{5\cdot 6\cdot 7} +\cdots$

Each integration brings a needed constant into the denominator. Then we can get an explicit expression for the sum by integrating the left side 3 times. This is very messy but Maxima (http://maxima.sourceforge.net) could handle it. The left side is:

$\mathrm{leftside}(x) = {{x^2\,\log \left(x^2+x+1\right)}\over{12}}+{{x\,\log \left(x^2+x+1 \right)}\over{3}}+{{\log \left(x^2+x+1\right)}\over{12}}-$

${{\sqrt{3} \,x^2\,\arctan \left({{2\,\sqrt{3}\,x}\over{3}}+{{\sqrt{3}}\over{3}} \right)}\over{6}}+{{\sqrt{3}\,\arctan \left({{2\,\sqrt{3}\,x}\over{3 }}+{{\sqrt{3}}\over{3}}\right)}\over{6}}-{{\log \left(1-x\right)\,x^ 2}\over{6}}+$

${{\sqrt{3}\,\arctan \left({{\sqrt{3}}\over{3}}\right)\,x ^2}\over{6}}+{{\log \left(1-x\right)\,x}\over{3}}-{{x}\over{2}}-{{ \log \left(1-x\right)}\over{6}}-{{\sqrt{3}\,\arctan \left({{\sqrt{3} }\over{3}}\right)}\over{6}}$

$\lim_{x\rightarrow 1}\ \mathrm{leftside}(x)={{\log 3}\over{2}}-{{1}\over{2}}\,$

$1+\frac{2}{2\cdot 3 \cdot 4} + \frac{2}{5\cdot 6\cdot 7} +\cdots=1+2\left({{\log 3}\over{2}}-{{1}\over{2}}\right)= \log 3 \qquad \square$

Retrieved from "http://www.efnet-math.org/w/Sol041406"