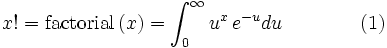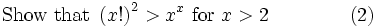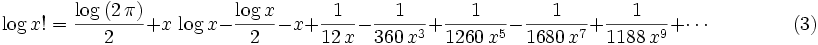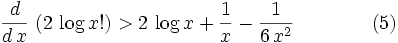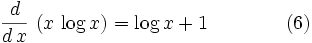Sol041706

Define for positive, real $x$ , not just integers:

$x!=\mathrm{factorial}\,(x)=\int_0^\infty u^x\,e^{-u}du\qquad\qquad(1)$

$\mbox{Show that }\left(x!\right)^2 > x^x \mbox{ for }x>2\,\qquad\qquad(2)$

Solution from landen

From the Stirling series for the log of the gamma function, equation 8, in this MathWorld (http://mathworld.wolfram.com/StirlingsSeries.html) article. We can obtain:

$\log x! = {{\log \left(2\,\pi\right)}\over{2}}+x\,\log x-{{\log x}\over{2}}-x+{{1}\over{12\,x}}-{{1}\over{360\,x^3 }}+{{1}\over{1260\,x^5}}-{{1}\over{1680\,x^7}}+{{1}\over{1188\,x^9}} +\cdots\,\qquad\qquad(3)$

Since equality holds in our proposition (2) in the limit at x=2, the series (3) cannot directly prove (2). Instead we can start at (2!)²=2², and prove that x!² has a larger derivative than x^x.

${{d}\over{d\,x}}\,\left(2\,\log x!\right)=2\,\log x+{{1}\over{x}}-{{1}\over{6\,x^2}}+{{1}\over{60\,x^4}}-{{1 }\over{126\,x^6}}+{{1}\over{120\,x^8}}-{{1}\over{66\,x^{10}}}+\cdots\qquad (4)$

${{d}\over{d\,x}}\,\left(2\,\log x!\right)>2\,\log x+{{1}\over{x}}- {{1}\over{6\,x^2}}\qquad \qquad (5)$

${{d}\over{d\,x}}\,\left(x\,\log x\right)=\log x+1\qquad\qquad (6)$

For x>2 Eqn. (4) can be truncated to give Ineq (5) by the properties of alternating decreasing series. Then the main proposition (2) follows by using a calculator on (5) or using a little theory on the simple expressions and comparing their derivatives. $\square$

Retrieved from "http://www.efnet-math.org/w/Sol041706"