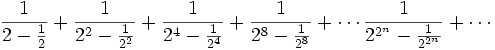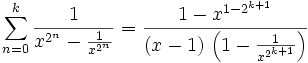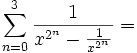Sol042706
Evaluate the sum:
Solution I from landen
It is easily proved by induction on k that:
The question is how to guess to prove that by induction. landen did a few numerical experiments and got, e.g.:
Once the pattern was clear it was easy to guess the sum and then prove it with induction. The limit 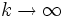 with
with 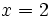 is
is