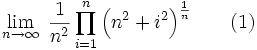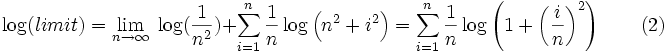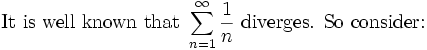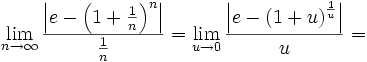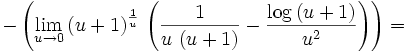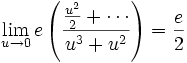Sol043006

Official Solutions

$\lim_{n\rightarrow\infty}\;\frac{1}{n^2} \prod_{i=1}^n{\left(n^2+i^2\right)^{\frac{1}{n}}}\qquad(1)$

By taking logs we can convert the problem to a sum:

$\log(limit)=\lim_{n\rightarrow\infty}\;\log(\frac{1}{n^2})+ \sum_{i=1}^n\frac{1}{n}\log\left(n^2+i^2\right)= \sum_{i=1}^n\frac{1}{n}\log\left(1+\left(\frac{i}{n}\right)^2\right)\qquad(2)$

Now we have a Riemann sum on the right of equation (2).

$\log(limit)=\int_0^1\log(1+x^2)\;dx=\log 2+{{\pi}\over{2}}-2\qquad(3)$

$limit = 2\,e^{{{\pi}\over{2}}-2}\qquad\square$

2. Does this sum converge:

$\sum_{n=1}^{\infty}\, \left| e - \left(1+\frac{1}{n}\right)^{n}\right|\qquad(1)$

This is a positive series so the limit comparison test (http://pirate.shu.edu/projects/reals/numser/t_lcomp.html) is often useful.

$\mbox{It is well known that }\sum_{n=1}^{\infty}\frac{1}{n}\mbox{ diverges. So consider:}$

$\lim_{n\rightarrow\infty}\frac{\left| e - \left(1+\frac{1}{n}\right)^{n}\right|}{\frac{1}{n}} = \lim_{u\rightarrow 0}\frac{\left| e - \left(1+u\right)^{\frac{1}{u}}\right|}{u} =$

$-\left(\lim_{u\rightarrow 0}{\left(u+1\right)^{{{1}\over{u}}}\, \left({{1}\over{u\,\left(u+1\right)}}-{{\log \left(u+1\right)}\over{ u^2}}\right)}\right)=$

$e\,\left(\lim_{u\rightarrow 0}{{{\left(u+1\right)\,\log \left(u+1 \right)-u}\over{u^3+u^2}}}\right)\mbox{ after one application of l}^\prime\mbox{H}\hat{\mathrm{o}}\mbox{pital and taking one limit}$

One way to continue is to expand the numerator in a short Taylor series:

$\lim_{u\rightarrow 0}e\left(\frac{{{u^2}\over{2}}+\cdots}{u^3+u^2}\right)= \frac{e}{2}$

Therefore, proposition in line (1) diverges by the limit comparison test. $\qquad\square$

Retrieved from "http://www.efnet-math.org/w/Sol043006"