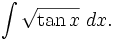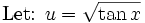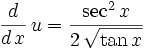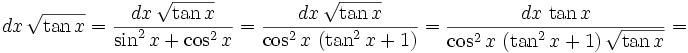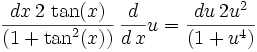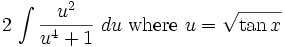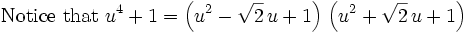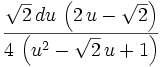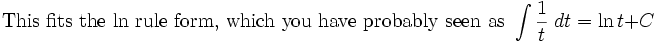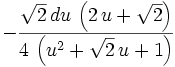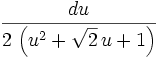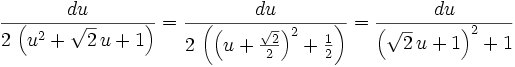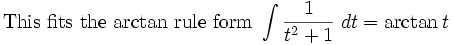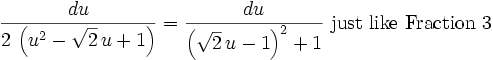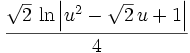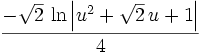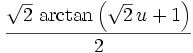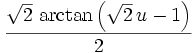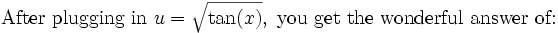Sol052706

The problem is to find

$\int {\sqrt{\tan x}}{\;dx}.$

$\mbox{Let: }u=\sqrt{\tan x}$

${{d}\over{d\,x}}\,u={{\sec ^2x}\over{2\,\sqrt{\tan x}}}$

$\mbox{Now, you have to transform }{\sqrt{\tan x}}{\;dx}\mbox{ into a more workable form.}$

$dx\,\sqrt{\tan x}={{dx\,\sqrt{\tan x}}\over{\sin ^2x+\cos ^2x}}={{dx \,\sqrt{\tan x}}\over{\cos ^2x\,\left(\tan ^2x+1\right)}}={{dx \,\tan x}\over{\cos ^2x\,\left(\tan ^2x+1\right)}\,\sqrt{\tan x}}=$

${{dx \, 2 \, \tan(x) }\over{ (1+\tan^2(x))}} \, {{d}\over{d\,x}}u= {{du \, 2u^2} \over {(1+u^4)}}$

So now we got:

$2\,\int {{{u^2}\over{u^4+1}}}{\;du}\mbox{ where } u=\sqrt{\tan x}$

$\mbox{Notice that }u^4+1=\left(u^2-\sqrt{2}\,u+1\right)\,\left(u^2+\sqrt{2}\,u+1 \right)$ How to factor this

Activate your partial fractions skills to get four fractions.

Fraction 1:

${{\sqrt{2}\,du\,\left(2\,u-\sqrt{2}\right)}\over{4\,\left(u^2- \sqrt{2}\,u+1\right)}}$

$\mbox{This fits the ln rule form, which you have probably seen as }\int {{{1}\over{t}}}{\;dt}=\ln t + C$

Fraction 2:

$-{{\sqrt{2}\,du\,\left(2\,u+\sqrt{2}\right)}\over{4\,\left(u^2+ \sqrt{2}\,u+1\right)}}$

This follows the same rule as Fraction 1. There are corresponding sign changes.

Fraction 3:

${{du}\over{2\,\left(u^2+\sqrt{2}\,u+1\right)}}$

The standard attack on this is to complete the square in the denominator to get an arctan integral.

${{du}\over{2\,\left(u^2+\sqrt{2}\,u+1\right)}}={{du}\over{2\,\left(\left(u+{{\sqrt{2}}\over{2}}\right)^2+{{1 }\over{2}}\right)}}={{du}\over{\left(\sqrt{2}\,u+1\right)^2+1}}$

$\mbox{This fits the arctan rule form }\int {{{1}\over{t^2+1}}}{\;dt}=\arctan t$

Fraction 4:

${{du}\over{2\,\left(u^2-\sqrt{2}\,u+1\right)}}={{du}\over{\left(\sqrt{2}\,u-1\right)^2+1}}\mbox{ just like Fraction 3}$

Now, comes the integration. The thing to know is that when you add up all the partial fractions, you get the original fraction. So, we have to integrate all the fractions, and add their integrals together.

Fraction 1 integrated is:

${{\sqrt{2}\,\ln\left| u^2-\sqrt{2}\,u+1\right|}\over{4 }}$

Fraction 2 integrated is:

${{-\sqrt{2}\,\ln\left| u^2+\sqrt{2}\,u+1\right|}\over{4 }}$

Fraction 3 integrated is:

${{\sqrt{2}\,\arctan \left(\sqrt{2}\,u+1\right)}\over{2}}$

Fraction 4 integrated is:

${{\sqrt{2}\,\arctan \left(\sqrt{2}\,u-1\right)}\over{2}}$

When you add all these together, you get the solution in terms of u. Don't forget to add your constant of integration.

$\mbox{After plugging in }u = \sqrt{\tan(x)},\mbox{ you get the wonderful answer of:}$

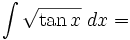
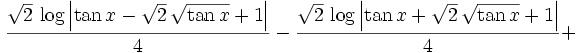
$\int {\sqrt{\tan x}}{\;dx}=$ ${{\sqrt{2}\,\log \left| \tan x-\sqrt{2}\,\sqrt{\tan x}+1\right| }\over{4}}-{{\sqrt{2}\,\log \left|\tan x+\sqrt{2}\,\sqrt{\tan x}+1 \right|}\over{4}}+$

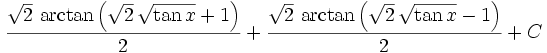
${{\sqrt{2}\,\arctan \left(\sqrt{2}\,\sqrt{\tan x}+ 1\right)}\over{2}}+{{\sqrt{2}\,\arctan \left(\sqrt{2}\,\sqrt{\tan x} -1\right)}\over{2}}+C$

And FINALLY, you are done.

This has been an i_c-Y presentation, and i_c-Y thanks you for trying this problem.

Typesetting in wiki math by Landen

Retrieved from "http://www.efnet-math.org/w/Sol052706"