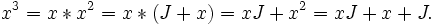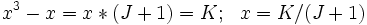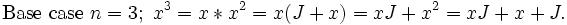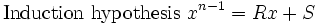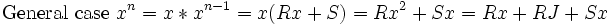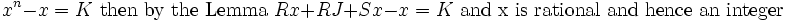Sol07032006

$frac(x) = frac(x2)$ implies $x 2 - x = J$ for some integer $J$

The values of $x$ which satisfy $x 2 - x = J$ are either integers or they are irrational. This is from the rational roots theorem (http://en.wikipedia.org/wiki/Rational_root_theorem).

Similarly $x 3 - x = K$ for some integer K. Combining the two equations we get

$x^3=x*x^2=x*(J+x)=xJ+x^2=xJ+x+J.\,$

$x^3-x=x*(J+1)=K; \ \ x=K/(J+1)$

Therefore $x$ is rational and hence an integer.

Lemma for the bonus problem.

$\mbox{Given }x^2-x=J, \ n>2, \mbox{ then } x^n\mbox{ can be written as a linear polynomial in }\mathbb{Z}[x]\,$

Proof by induction on $n$

$\mbox{Base case }n=3;\ x^3=x*x^2=x(J+x)=xJ+x^2=xJ+x+J.$

$\mbox{Induction hypothesis }x^{n-1}=Rx+S\,$

$\mbox{General case }x^n=x*x^{n-1}=x(Rx + S)=Rx^2 +Sx = Rx+RJ+Sx\,$

$\square$

Bonus Problem Main Proof

$x^n-x=K \mbox{ then by the Lemma }Rx+RJ+Sx-x=K\mbox{ and x is rational and hence an integer}\,$

$\square$

Retrieved from "http://www.efnet-math.org/w/Sol07032006"