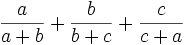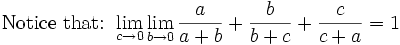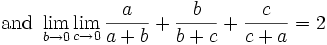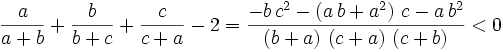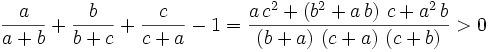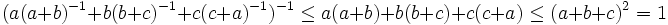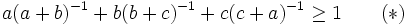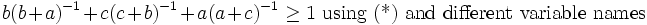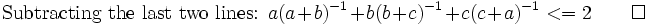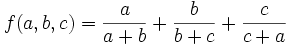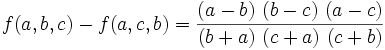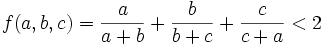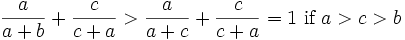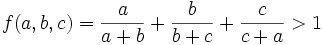SolAug0706

For 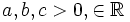$a,b,c >0, \in \mathbb{R}$ find the upper(LUB) and lower(GLB) limits of:

$\frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}$

Solution I by landen

As is common in a homogenous expression we can take $a + b + c = 1$ without loss of generality.

$\mbox{Notice that: }\lim_{c\rightarrow 0} \lim_{b\rightarrow 0}\frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}=1$

$\mbox{and }\lim_{b\rightarrow 0} \lim_{c\rightarrow 0}\frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}=2$

Sometimes these expressions have a max or min out in the middle at: $a = b = c .$ In this case this is 3/2 so we make a hypothesis that the GLB is 1 and the LUB is 2.

$\frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}-2={{-b\,c^2-\left(a\,b+a^2\right)\,c-a\,b^2}\over{\left(b+a\right)\, \left(c+a\right)\,\left(c+b\right)}}<0$

So we can't reach 2 but we already know it is a possible limit so 2 is the LUB.

$\frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}-1={{a\,c^2+\left(b^2+a\,b\right)\,c+a^2\,b}\over{\left(b+a\right)\, \left(c+a\right)\,\left(c+b\right)}}>0$

Now we know we can't reach 1 on the lower side so 1 is the GLB since it is a limit. $\square$

Solution II by bumpero, int-e, and landen

Using the weighted power mean (http://planetmath.org/encyclopedia/WeightedPowerMean.html) with weights $a, b, c$ with $a + b + c = 1,$ and powers 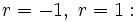$r=-1,\ r=1:$

$(a(a+b)^{-1} + b(b+c)^{-1} + c(c+a)^{-1})^{-1} \le a(a+b)+b(b+c)+c(c+a)\le (a+b+c)^2 = 1\,$

$a(a+b)^{-1} + b(b+c)^{-1} + c(c+a)^{-1}\ge 1\qquad (*)\,$

$\mbox{Notice: }a(a+b)^{-1} + b(b+c)^{-1} + c(c+a)^{-1}+b(b+a)^{-1} + c(c+b)^{-1} + a(a+c)^{-1}=3\,$

$b(b+a)^{-1} + c(c+b)^{-1} + a(a+c)^{-1} \ge 1 \mbox{ using (*) and different variable names}\,$

$\mbox{Subtracting the last two lines: }a(a+b)^{-1} + b(b+c)^{-1} + c(c+a)^{-1}<=2\qquad \square\,$

Solution III by landen under construction

$f(a,b,c)=\frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}$

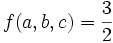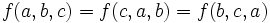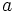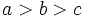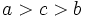Notice that $f(a,b,c)=\frac{3}{2}$ if any two of the variables are equal. So, any case of equality is easy. Also, $f(a,b,c)=f(c,a,b)=f(b,c,a)\,$ . This equality property is called cyclic symmetry. We can take $a\,$ to be the largest variable without loss of generality. Either, $a>b>c\,$ or $a>c>b\,$ for all unequal cases.

$f(a,b,c)-f(a,c,b)={{\left(a-b\right)\,\left(b-c\right)\,\left(a-c\right)}\over{ \left(b+a\right)\,\left(c+a\right)\,\left(c+b\right)}}$

The previous equation tells us that for determinining the maximum of 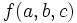$f(a,b,c)\,$ we can consider the case 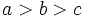$a>b>c\,$ only. The sign of 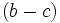$(b-c)\,$ governs whether 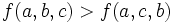$f(a,b,c)>f(a,c,b)\,$ or not. In finding the max of 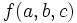$f(a,b,c)\,$ we do not need to consider the case 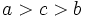$a>c>b\,$ . In finding the min of 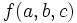$f(a,b,c)\,$ we do not need to consider the case $a>b>c\,$ .

$\frac{a}{a+b}+\frac{c}{c+a} < \frac{a}{a+c}+\frac{c}{c+a}=1 \mbox{ if }a>b>c$

$f(a,b,c)=\frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}<2$

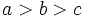Then for the lower bound:

$\frac{a}{a+b}+\frac{c}{c+a} > \frac{a}{a+c}+\frac{c}{c+a}=1 \mbox{ if }a>c>b$

$f(a,b,c)=\frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}>1$

$\qquad \square$

Retrieved from "http://www.efnet-math.org/w/SolAug0706"