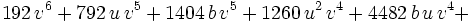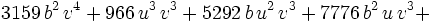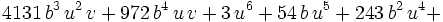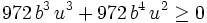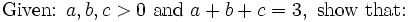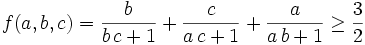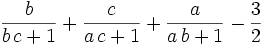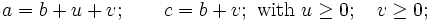SolAug1806

from Prof. Vasile Crîtoaje

$\mbox{Given: }a,b,c>0\mbox{ and }a+b+c=3,\mbox{ show that:}\,$

$f(a,b,c)={{b}\over{b\,c+1}}+{{c}\over{a\,c+1}}+{{a}\over{a\,b+1}}\ge\frac{3}{2}$

Solution by landen with help from int-e

int-e helped a lot by pointing out how obnoxious this function is and that all the methods we had been trying wouldn't work. landen reluctantly got out Maxima (http://maxima.sourceforge.net). Somebody find a cute proof!

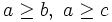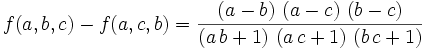
Proof: Since we have cyclic symmetry we can assume $a\ge b,\ a\ge c$ without loss of generality. Also notice that: $f(a,b,c)-f(a,c,b)={{\left(a-b\right)\,\left(a-c\right)\,\left(b-c\right)}\over{\left( a\,b+1\right)\,\left(a\,c+1\right)\,\left(b\,c+1\right)}}$

If 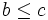$b\le c\,$ , then 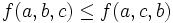$f(a,b,c) \le f(a,c,b)\,$ . We want a lower bound for 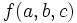$f(a,b,c)\,$ , it is sufficient to consider 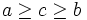$a\ge c \ge b$ since the lower bound of 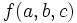$f(a,b,c)\,$ will be a lower bound for the other permutations of $\{a,b,c\}\,$ . Sometimes this helps with cyclic symmetry.

Next, we, aka Maxima, homogenize:

${{b}\over{b\,c+1}}+{{c}\over{a\,c+1}}+{{a}\over{a\,b+1}}-\frac{3}{2}$

Replace 1 by 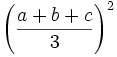$\left( \frac{a+b+c}{3}\right)^2$ in the denominator to make the denominator a quadratic. Then multiply the numerator by 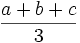$\frac{a+b+c}{3}$ to make it a quadratic also. Then get a common denominator. After this manipulation we get an equivalent problem:
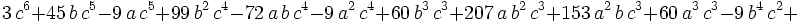
$3\,c^6+45\,b\,c^5-9\,a\,c^5+99\,b^2\,c^4-72\,a\,b\,c^4-9\,a^2\,c^4+ 60\,b^3\,c^3+207\,a\,b^2\,c^3+153\,a^2\,b\,c^3+60\,a^3\,c^3-9\,b^4\, c^2+$
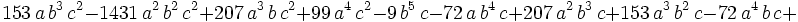
$153\,a\,b^3\,c^2-1431\,a^2\,b^2\,c^2+207\,a^3\,b\,c^2+99\,a^4\,c ^2-9\,b^5\,c-72\,a\,b^4\,c+207\,a^2\,b^3\,c+153\,a^3\,b^2\,c-72\,a^4 \,b\,c+$
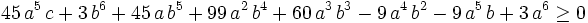
$45\,a^5\,c+3\,b^6+45\,a\,b^5+99\,a^2\,b^4+60\,a^3\,b^3-9\,a^4 \,b^2-9\,a^5\,b+3\,a^6\ge 0$

This is a polynomial with every term of degree 6 and it is homogeneous which is usually a simplification of a constrained inequality. Next, we can set:

$a=b+u+v;\qquad c=b+v; \mbox{ with }u\ge 0;\quad v\ge0;$

Maxima easily does this substitution and the result is:
$192\,v^6+792\,u\,v^5+1404\,b\,v^5+1260\,u^2\,v^4+4482\,b\,u\,v^4+$
$3159\,b^2\,v^4+966\,u^3\,v^3+5292\,b\,u^2\,v^3+7776\,b^2\,u\,v^3+$
$2916\,b^3\,v^3+369\,u^4\,v^2+2727\,b\,u^3\,v^2+7290\,b^2\,u^2\,v^2+$
$5103\,b^3\,u\,v^2+972\,b^4\,v^2+63\,u^5\,v+621\,b\,u^4\,v+2673\,b^2\,u^3\,v+$
$4131\,b^3\,u^2\,v+972\,b^4\,u\,v+3\,u^6+54\,b\,u^5+243\,b^2 \,u^4+$
$972\,b^3\,u^3+972\,b^4\,u^2 \ge 0$

$\square$

Retrieved from "http://www.efnet-math.org/w/SolAug1806"