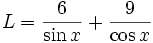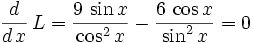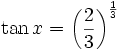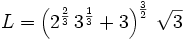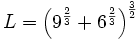SolDec0405

Call the length of the pipe $L$ and the angle the pipe makes with the side of the 6ft wide hall $x$ . L touches the inside corner where the halls join so we have:

$L={{6}\over{\sin x}}+{{9}\over{\cos x}}\,$

If $L$ is too long it can't round the corner, so we actually want the shortest pipe that can touch both walls of both halls. Then, as $x$ increases, the pipe could be lengthened and not touch so it will not bind up. So we differentiate $L$ and set the derivative to 0 to find a critical point.

${{d}\over{d\,x}}\,L = {{9\,\sin x}\over{\cos ^2x}}-{{6\,\cos x}\over{\sin ^2x}}=0$

$\tan x = \left(\frac{2}{3}\right)^{\frac{1}{3}}\,$

$L=\left(2^{{{2}\over{3}}}\,3^{{{1}\over{3}}}+3\right)^{{{3}\over{2}}} \,\sqrt{3}$

This expression for $L$ was found by Maxima software. Polytope wrote it in a much more symmetrical way:

$L=\left(9^{{{2}\over{3}}}+6^{{{2}\over{3}}}\right)^{{{3}\over{2}}}$

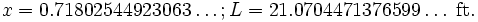
$x= 0.71802544923063\dots; L = 21.0704471376599\dots \mbox{ ft}.$

The messy second derivative of $L$ is positive so we have found a minimum.

Retrieved from "http://www.efnet-math.org/w/SolDec0405"