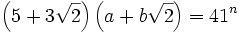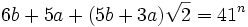SolFeb1306

Under Construction.

Find all integers m, n such that

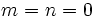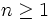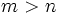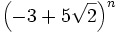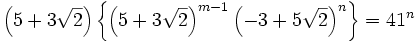
There is the obvious solution $m=n=0\,$ . Assume we have a solution $n\ge 1\,$ , then $m>n\,$ because $m\,$ is operating on a smaller number. If we multiply both sides by $\left(-3 + 5 \sqrt{2}\right)^n\,$ , rearrange the parentheses a little on the left, and simplify the right we get: $\left(5 + 3 \sqrt{2}\right)\left\{ \left(5 + 3 \sqrt{2}\right)^{m-1} \left(-3 + 5 \sqrt{2}\right)^n\right\}=41^n\,$

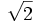The complicated expression in $\{\,\}\,$ on the left is of the form $a+b\sqrt{2}\,$ with integers a and b if it were multiplied out. So we consider:

$\left(5 + 3 \sqrt{2}\right) \left(a + b \sqrt{2}\right) =41^n\,$

$6b+5a + (5b+3a)\sqrt{2} = 41^n\,$

Since $\sqrt{2}\,$ is irrational,

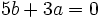
$5b+3a=0\,$

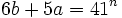$6b+5a=41^n\,$ and then combining the equations and eliminating $a\,$ :

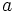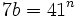
$7b=41^n\,$

This produces a contradiction because 41 is a prime and is not divisible by 7. Therefore, there are no solutions with 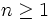$n\ge 1\,$ .

Retrieved from "http://www.efnet-math.org/w/SolFeb1306"