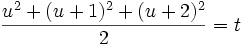SolFeb14

Show that a² + b² + c² = (a − b)(b − c)(c − a) has infinitely many integral solutions. Here are 4 of the solutions found by landen's computer. (-1,0,1), (7,14,21),(75,100,125), and (275,330,385). These are interesting because they are not relatively prime and form part of an arithmetic series. If we factor out the common factor in each we get: (-1,0,1), 7(1,2,3), 25(3,4,5), 55(5,6,7). Inept proposed that there are infinitely many solutions of the form t(u,u + 1,u + 2) with u any odd number. I(landen) don't know how Inept came to this idea but it is cool. Inserting this hypothesis into the problem and dividing by 2t² we get:

Since u is odd, t is an integer and immediately we can make infinitely many solutions. Arne Smeets solved the problem and got the same set of solutions but with different variables. Many of the solutions are not in an arithmetic series. It would be interesting to know if there are infinitely many of them and how to generate all the solutions. There is one positive solution with relatively prime numbers in the list: [1063, 1184, 1321] gcd=1

Here is a more extensive list:
[-1, 1, 2] gcd=1
[-2, -1, 1] gcd=1
[-1, 0, 1] gcd=1
[7, 14, 21] gcd=7
[55, 85, 100] gcd=5
[60, 75, 105] gcd=15
[75, 100, 125] gcd=25
[115, 161, 184] gcd=23
[155, 250, 265] gcd=5
[175, 205, 260] gcd=5
[259, 266, 497] gcd=7
[275, 330, 385] gcd=55
[679, 776, 873] gcd=97
[650, 715, 845] gcd=65
[775, 790, 1205] gcd=5
[891, 1053, 1134] gcd=81
[736, 943, 989] gcd=23
[918, 999, 1161] gcd=27
[1063, 1184, 1321] gcd=1
[1150, 1175, 1625] gcd=25
[860, 1195, 1225] gcd=5
[1359, 1510, 1661] gcd=151
[1687, 3829, 3836] gcd=7
[2387, 2604, 2821] gcd=217
[2415, 2445, 3300] gcd=15
[2416, 2567, 2869] gcd=151
[2450, 2891, 2989] gcd=49
[2975, 3325, 3500] gcd=175
[2140, 2995, 3025] gcd=5
[3263, 3549, 3796] gcd=13
[3276, 3523, 3809] gcd=13