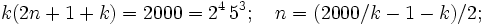SolFeb2005

If we add together k consecutive numbers starting at n + 1, twice, mixing increasing and decreasing we get:

((n + 1) + (n + k)) + ((n + 2) + (n + 1 + (k − 2))...((n + k) + (n + 1)) = 2000

There are k terms each of size 2n+1+k so we have:

k(2n+1+k)=2000=2^4\,5^3;\quad n=(2000/k-1-k)/2;

Notice that if k is odd,then (2n + 1 + k) is even. Also if k is even then then (2n + 1 + k) is odd. The only feasible values of k are 1,5,25,125, and 16. k=1 leads to a trivial solution and k=125 makes n negative. So the solutions that work are:
198 to 202 n=197 k=5
55 to 70 n=54 k=16
28 to 52 n=27 k=25

Retrieved from "http://www.efnet-math.org/w/SolFeb2005"