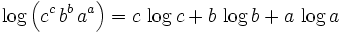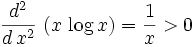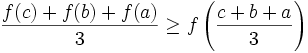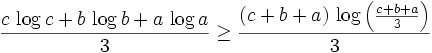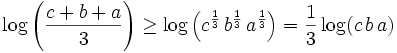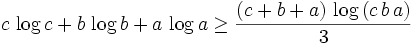SolFeb2205
Solution by landen
Show that if  then
then
It looks like logs will help
Define: 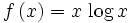
Since the second derivative is positive, 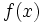 is convex. For a convex function we can apply Jensen's (http://www.engineering.usu.edu/classes/ece/7680/lecture2/node5.html)
inequality, the average of the function at points is greater than or
equal to the function evaluated at the average of the points:
is convex. For a convex function we can apply Jensen's (http://www.engineering.usu.edu/classes/ece/7680/lecture2/node5.html)
inequality, the average of the function at points is greater than or
equal to the function evaluated at the average of the points:
Since 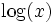 is monotonically increasing we can use the arithmetic-geometric mean inequality (http://www.cs.utexas.edu/users/misra/Notes.dir/Arithmetic,GeometricMean.pdf):
is monotonically increasing we can use the arithmetic-geometric mean inequality (http://www.cs.utexas.edu/users/misra/Notes.dir/Arithmetic,GeometricMean.pdf):
Since 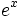 is monotonically increasing we can exponentiate both sides to get:
is monotonically increasing we can exponentiate both sides to get:
Q.E.D.