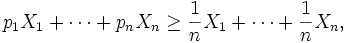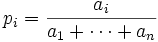SolFeb2205 HL
Claim: For any positive numbers 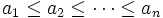 ,
,
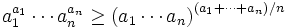 .
.
Proof: We solve this using an averaging
argument. Taking logs and dividing both sides by  , it suffices to show that
, it suffices to show that
where
and 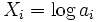 . Since the
. Since the
 are non-decreasing, so are the
are non-decreasing, so are the 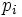 and the
and the 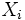 . All we
need show is that any such weighted average, where the weights
increase as the numbers
increase, is bounded below by the arithmetic mean:
. All we
need show is that any such weighted average, where the weights
increase as the numbers
increase, is bounded below by the arithmetic mean:
Since the  and
and  , we can apply one of Chebyshev's inequalities (http://planetmath.org/encyclopedia/ChebyshevsInequality.html) to this.
, we can apply one of Chebyshev's inequalities (http://planetmath.org/encyclopedia/ChebyshevsInequality.html) to this.
Since  the claim is immediately established.
the claim is immediately established.