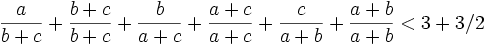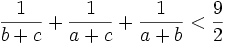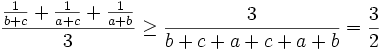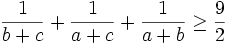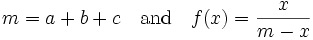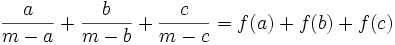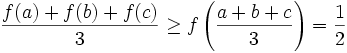SolFeb2506
bonus problem: show for a,b,c > 0:
Solution I For a proof by contradiction approach assume:
Multiplying 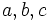 by a positive constant
by a positive constant 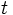 does not change the left side of the inequality. For convenience we can take
does not change the left side of the inequality. For convenience we can take 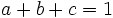
Next we show that this inequality cannot hold.
From the reciprocal of the harmonic-arithmetic mean inequality (http://planetmath.org/encyclopedia/ProofOfArithmeticGeometricHarmonicMeansInequality.html), we get:
So the original inequality is true by proof by contradiction.
Solution II For a proof using a little calculus Define
Rewrite the left side of the inequality:
Taking the second derivative of 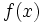 :
:
Since the second derivative is positive for 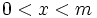 , we find that
, we find that 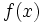 is convex. For a convex function we can apply Jensen's (http://www.engineering.usu.edu/classes/ece/7680/lecture2/node5.html)
inequality, the average of the function at points is greater than or
equal to the function evaluated at the average of the points:
is convex. For a convex function we can apply Jensen's (http://www.engineering.usu.edu/classes/ece/7680/lecture2/node5.html)
inequality, the average of the function at points is greater than or
equal to the function evaluated at the average of the points:
Multiplying by 3 establishes the inequality. Q.E.D.