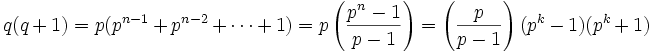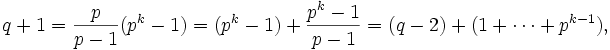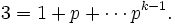SolFeb28
Claim: There is only one solution to
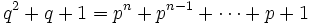 for p,q primes, n > 2 even.
for p,q primes, n > 2 even.
Proof: (Due to HiLander) Suppose (p,q,n) satisfies the claim. Since n is even, n = 2k for some k, and
since n > 2, we have k > 1 and 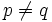 . Subtracting 1 from
both sides of the formual, we factor both sides:
. Subtracting 1 from
both sides of the formual, we factor both sides:
Suppose first that 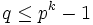 . Then
. Then
a contradiction.
Now suppose q > pk + 1. Since q is prime, and we know 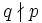 and
and 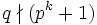 , we must have
, we must have  , another contradiction.
, another contradiction.
Therefore 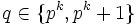 . If q = pk, then k = 1 since
both are prime, so instead we have q = pk + 1. But that means
. If q = pk, then k = 1 since
both are prime, so instead we have q = pk + 1. But that means
and so
Since 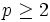 and
and 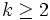 , this implies both hold at equality,
else the RHS of our last equation is too large. From this, we get n = 2k = 4,
and q = pk + 1 = 5, so (2,5,4) is the only solution
(p,q,n).
, this implies both hold at equality,
else the RHS of our last equation is too large. From this, we get n = 2k = 4,
and q = pk + 1 = 5, so (2,5,4) is the only solution
(p,q,n).