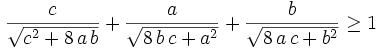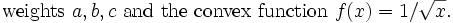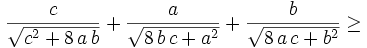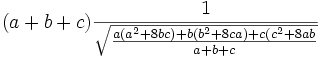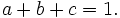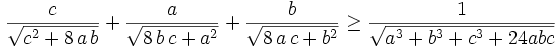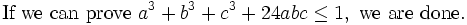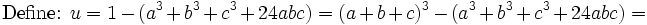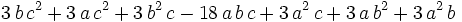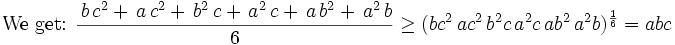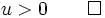SolJul2406

Show that for all positive reals $a, b, c,$

${{c}\over{\sqrt{c^2+8\,a\,b}}}+{{a}\over{\sqrt{8\,b\,c+a^2}}}+{{b }\over{\sqrt{8\,a\,c+b^2}}}\ge 1$

We can apply Jensen's inequality (http://planetmath.org/encyclopedia/JensensInequality.html) with

$\mbox{weights }a,b,c\mbox{ and the convex function }f(x)=1/\sqrt{x}.\,$

${{c}\over{\sqrt{c^2+8\,a\,b}}}+{{a}\over{\sqrt{8\,b\,c+a^2}}}+{{b }\over{\sqrt{8\,a\,c+b^2}}}\ge$

$(a+b+c)\frac{1}{\sqrt{\frac{a(a^2+8bc)+b(b^2+8ca)+c(c^2+8ab}{a+b+c}}}$

Since all three variables may be multiplied by a constant without altering the value of the expression, without loss of generality we may take:

$a+b+c=1.\,$

${{c}\over{\sqrt{c^2+8\,a\,b}}}+{{a}\over{\sqrt{8\,b\,c+a^2}}}+{{b }\over{\sqrt{8\,a\,c+b^2}}}\ge\frac{1}{\sqrt{a^3+b^3+c^3+24abc}}$

$\mbox{If we can prove }a^3+b^3+c^3+24abc \le 1,\mbox{ we are done.}$

$\mbox{Define: }u = 1-(a^3+b^3+c^3 + 24abc)=(a+b+c)^3-(a^3+b^3+c^3 + 24abc)=\,$

$3\,b\,c^2+3\,a\,c^2+3\,b^2\,c-18\,a\,b\,c+3\,a^2\,c+3\,a\,b^2+3\,a^ 2\,b$

From Arithmetic Mean - Geometric Mean Inequality (http://planetmath.org/?op=getobj&from=objects&name=ArithmeticGeometricMeansInequality)

$\mbox{We get: }\frac{\,b\,c^2+\,a\,c^2+\,b^2\,c+\,a^2\,c+\,a\,b^2+\,a^ 2\,b}{6}\ge (bc^2\,ac^2\,b^2c\,a^2c\,ab^2\,a^2b)^{\frac{1}{6}}=abc$

$u>0\qquad \square$