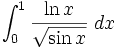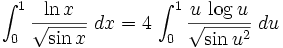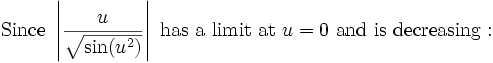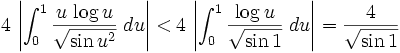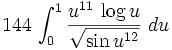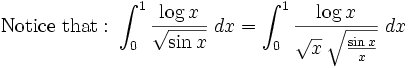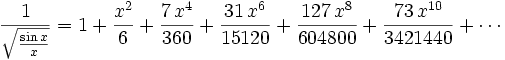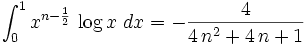SolMar1606

Prove this integral converges:

$\int_{0}^{1}{{{\ln x}\over{\sqrt{\sin x}}}\;dx}$

Then for real fun use a computer or your favorite calculator to estimate the integral to a bunch of decimal places. See how many you can do and if you can tell how accurate your answer is.

This integral has no primitive function that can be written in closed form in elementary functions. However, it still helps to use substitution on it. Let $x = u 2$ :

$\int_{0}^{1}{{{\ln x}\over{\sqrt{\sin x}}}\;dx}=4\,\int_{0}^{1}{{{u\,\log u}\over{\sqrt{\sin u^2}}}\;du}$

$\mathrm{Since\ }\left| \frac{u}{\sqrt{\sin(u^2)}}\right|\mathrm{\ has \ a \ limit\ at \ }u=0\mathrm{\ and\ is\ decreasing:}$

$4\,\left|\int_{0}^{1}{{{u\,\log u}\over{\sqrt{\sin u^2}}}\;du}\right|< 4\,\left|\int_{0}^{1}{{{\log u}\over{\sqrt{\sin 1}}}\;du}\right|={{4}\over{\sqrt{\sin 1}}}$

This establishes convergence. $\square$

Everybody seems to be taught Simpson's Rule (http://en.wikipedia.org/wiki/Simpson's_rule) for numerical integration. It is not a very good method but is traditional to teach. Recall that the error estimate needs the fourth derivative of the function to be integrated. Even after the substitution above, the fourth derivative is not bounded. However the substitution $x = u 12$ does give us a bounded fourth derivative.

$144\,\int_{0}^{1}{{{u^{11}\,\log u}\over{\sqrt{\sin u^{12}}}}\;du}$

So if anybody wanted to try Simpson's rule they could get an error estimate using this substitution. landen used Pari/GP (http://pari.math.u-bordeaux.fr/) to do the numerical integral after this substitution and got: -4.013654550392145413562759893629. Pari uses several Romberg (http://library.lanl.gov/numerical/bookcpdf/c4-3.pdf)-like techniques with an iterative accuracy improvement. Galois used Mathematica (http://www.wolfram.com/products/mathematica/index.html) and got: -4.013654550392145413562759893629088498737. Mathematica did not require the user to do a substitution if the recursion depth has been limited with a command. With the substitution, $x = u 8$ , limiting the depth was not necessary. Evidently mathematica is smart enough to modify the integral itself.

Polytope reported that Maple (http://www.maplesoft.com/) solved the problem and needed no help.

landen also did a homebrew numerical integration with known accuracy without using mysterious methods in CAS packages.

$\mathrm{Notice\ that:\ }\int_{0}^{1}{{{\log x}\over{\sqrt{\sin x}}}\;dx}=\int_{0}^{1}{{{ \log x}\over{\sqrt{x}\,\sqrt{{{\sin x}\over{x}}}}}\;dx}$

And using Taylor expansion:

${{1}\over{\sqrt{{{\sin x}\over{x}}}}}=1+{{x^2}\over{6}}+{{7\,x^4 }\over{360}}+{{31\,x^6}\over{15120}}+{{127\,x^8}\over{604800}}+{{73 \,x^{10}}\over{3421440}}+\cdots$

$\int_{0}^{1}{x^{n-{{1}\over{2}}}\,\log x\;dx}=-{{4}\over{4\,n^2+4\, n+1}}$

We can insert the Taylor series into our integral and integrate term by term to as many terms as we care to compute. Notice the the sum of the terms can be summed exactly as rational numbers. So no roundoff error at this stage. The error we have comes from trucating the Taylor series. Since the Taylor series has all positive coefficients the worst error occurs for $x = 1$ . We can use the Lagrange form of the remainder and worst case bound our error by computing the highest derivative of our function at $x = 1$ . There is roundoff in this calculation but we only need the order of magnitude correct. I wrote a Pari program which, given a number of terms to use. Calculates the rational number for the answer and then floats that. It also determines a lower bound on the number of correct digits. The error estimate could be improved with more analysis:

integral =
-4.013654550392145413562759893629088498737343618749054915657748602169988103598385433034839782722381382
guaranteed digits = 100

Here is the Pari program to do the number crunching in case Karlsen or anybody with a good computer wants to experiment.

singular(nterms)=
{
\\ nterms=301 will give 100 correct digits
default(seriesprecision,nterms);
default(realprecision,nterms);
maxpower=nterms-1; \\ sets the accuracy in the taylor series.
ts=truncate(taylor(sqrt(x/sin(x)),x)); \\ this has no roundoff error, it is rational
\\ts has all positive terms so all derivatives are increasing also.
valueit=0;
forstep(k=maxpower,0,-1,valueit=(valueit-polcoeff(ts,k)*4/(4*k^2+4*k+1)));
\\ still no roundoff error.

\\ ers only needs enough accuracy to get the ndigits correct.
\\ ers will have roundoff error because sin(1) is transcendental.
ers=truncate(taylor(sqrt((1+x)/sin(1+x)),x)); \\ expand about 1 to get the max error.
\\ maxerror is at 1 because all derivatives are in increasing in [0,1]
maxerror=polcoeff(ers,maxpower)*1.; \\Lagrange form of the error
default(realprecision,16);
\\print("maxerror = ",maxerror);

ndigits=floor((-log(maxerror))/log(10));
default(realprecision,ndigits);
print("integral = ",valueit*1.);
print("guaranteed digits = ",ndigits);\\ output routines rounds the rational.
}

Retrieved from "http://www.efnet-math.org/w/SolMar1606"