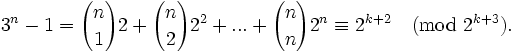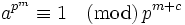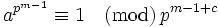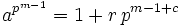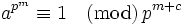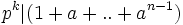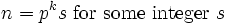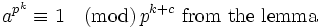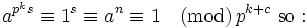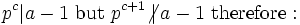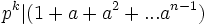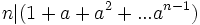SolProb031006

from dedekind rated: needs no advanced math

Find all n such that 2n divides 3n − 1.

Solution by Inept

Let n = 2km where m is odd. Then

3^n-1={n \choose 1}2+{n \choose 2}2^2+...+{n \choose n}2^n \equiv 2^{k+2} \pmod{2^{k+3}}.

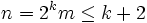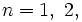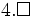
Therefore, n=2^k m\leq k+2 implying m = 1 and k = 0, k = 1, or k = 2, i.e., n=1,\ 2, or 4. \square

from Karlsen

Let a and n be positive integers. Suppose that n | (a − 1)2006.

Show that n | (1 + a + .. + an − 1).

Solution from nerdy2 and edited by landen

Factor n completely into powers of distinct primes. Suppose that pk is the factor of n for the prime p. k is the number of times p occurred in the factorization of n. It is sufficient to show that pk | (1 + a + .. + an − 1). The same argument can be repeated for each distinct prime to establish divisibility by n.

Since p is a prime, p | (a − 1). Factor a − 1 completely into distinct primes and suppose p^c is the power of p in the factorization of a − 1.

c \ge 1.

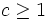Lemma

a^{p^m} \equiv 1 \quad\mathrm{(mod)}\,p^{m+c}

This is proved by induction on m. For the base case, m = 0:

a^{p^0} \equiv a \equiv 1 \quad\mathrm{(mod)}\,p^{c}

Next we assume:

a^{p^{m-1}} \equiv 1 \quad\mathrm{(mod)}\,p^{m-1+c}

For some integer r:

a^{p^{m-1}} = 1 + r\,p^{m-1+c}

If we raise both sides of the equation to the p power and use the binomial theorem on the right:

a^{p^{m}} = 1 + pr\,p^{m-1+c}+ ... p^{p(m-1+c)}=1+r\,p^{m+c} + \mathrm{higher \ powers\ of\ } p
a^{p^{m}} \equiv 1 \quad\mathrm{(mod)}\,p^{m+c}

\square


Main Proposition Show that:

p^k|(1+a+..+a^{n-1})\,
n=p^ks \mathrm{\ for\ some\ integer\ }s
a^{p^{k}} \equiv 1 \quad\mathrm{(mod)}\,p^{k+c}\mathrm{\ from\ the\ lemma}\,
a^{p^{k}s} \equiv 1^s \equiv a^n \equiv 1 \quad\mathrm{(mod)}\,p^{k+c}\mathrm{\ so:}\,
p^{k+c}|a^n-1 = (a-1)(1+a+a^2+...a^{n-1})\,
p^c | a-1 \mathrm{\ but\ }p^{c+1}\not | \,a-1\mathrm{\ therefore:}\,
p^{k}|(1+a+a^2+...a^{n-1})\,

We can repeat this argument for any other primes dividing n and get:

n|(1+a+a^2+...a^{n-1})\,

\square

Retrieved from "http://www.efnet-math.org/w/SolProb031006"