SolSep0106

Problem: 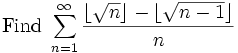$\mbox{Find }\sum_{n=1}^\infty \frac{\lfloor \sqrt{n}\rfloor - \lfloor \sqrt{n-1}\rfloor}{n}$

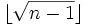Solution: If we look at the first terms (30 or so), we see that most of the terms are 0. The only time we have non-zero terms are when $n$ is a square. This is because $\lfloor \sqrt{n}\rfloor\,$ is bigger than $\lfloor \sqrt{n-1}\rfloor$ only when $n$ is square. If we take away the terms that are zero, we end up with

$1 + \frac{1}{4} + \frac{1}{9} + \frac{1}{16} + \ldots = \sum_{n=1}^\infty \frac{1}{n^2}$

which is a famous sum (http://en.wikipedia.org/wiki/Riemann_zeta_function#Values_at_the_integers). It is equal to 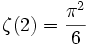$\zeta{(2)} = \frac{\pi^2}{6}\,$ .

Retrieved from "http://www.efnet-math.org/w/SolSep0106"