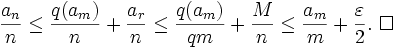SolSept0911-2
Let 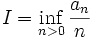 . We show that for any
. We show that for any 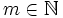 , any
, any  , there is an
, there is an 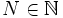 with
with 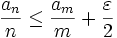 for all n > N. By
choosing m so that
for all n > N. By
choosing m so that 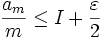 , we get that
, we get that 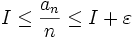 , and hence
, and hence
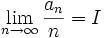 as claimed.
as claimed.
Let 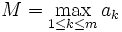 , and choose
, and choose 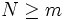 so that
so that
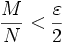 . Let n > N. By long
division, we can write n = qm + r, where
. Let n > N. By long
division, we can write n = qm + r, where  , and
since n > m,
, and
since n > m, 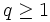 . Then
. Then 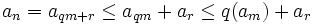 (by repeated applications of subadditivity), so
(by repeated applications of subadditivity), so