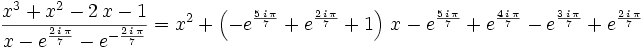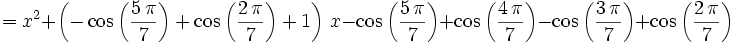Soljan1706

From landen

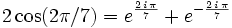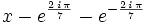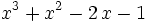Notice that $2\cos(2\pi/7)=e^{{{2\,i\,\pi}\over{7}}}+e^ {- {{2\,i\,\pi}\over{7}} }$ . If this is a root then $x-e^{{{2\,i\,\pi}\over{7}}}-e^ {- {{2\,i\,\pi}\over{7}} }$ will divide $x^3+x^2-2\,x-1$ .

So we proceed by just doing the long division and it works and we get no remainder.

$\frac{x^3+x^2-2\,x-1}{x-e^{{{2\,i\,\pi}\over{7}}}-e^ {- {{2\,i\,\pi}\over{7}} }}= x^2+\left(-e^{{{5\,i\,\pi}\over{7}}}+e^{{{2\,i\,\pi}\over{7}}}+1 \right)\,x-e^{{{5\,i\,\pi}\over{7}}}+e^{{{4\,i\,\pi}\over{7}}}-e^{{{ 3\,i\,\pi}\over{7}}}+e^{{{2\,i\,\pi}\over{7}}}$

$=x^2+\left(-\cos \left({{5\,\pi}\over{7}}\right)+\cos \left({{2\,\pi }\over{7}}\right)+1\right)\,x-\cos \left({{5\,\pi}\over{7}}\right)+ \cos \left({{4\,\pi}\over{7}}\right)-\cos \left({{3\,\pi}\over{7}} \right)+\cos \left({{2\,\pi}\over{7}}\right)$

As a bonus we could use the quadratic formula on the quadratic and get the other two roots which happen to be real also.

Retrieved from "http://www.efnet-math.org/w/Soljan1706"