Solnov1405

From landen.

Here is a general solution in integers. Two basic equations are needed. 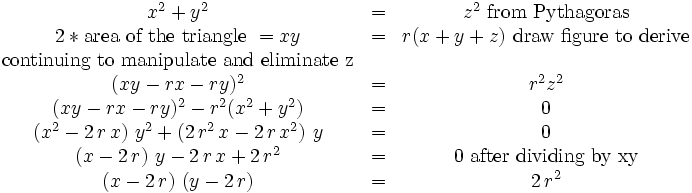$\begin{matrix} x^2+y^2 &=& z^2 \mbox{ from Pythagoras}\\ 2*\mbox{area of the triangle } = xy &=& r(x+y+z)\mbox{ draw figure to derive}\\ \mbox{continuing to manipulate and eliminate z}\\ (xy -rx -ry)^2 &=&r^2z^2\\ (xy -rx -ry)^2 -r^2(x^2+y^2) &=& 0\\ \left(x^2-2\,r\,x\right)\,y^2+\left(2\,r^2\,x-2\,r\,x^2\right)\,y &=& 0\\ \left(x-2\,r\right)\,y-2\,r\,x+2\,r^2&=&0\mbox{ after dividing by xy}\\ \left(x-2\,r\right)\,\left(y-2\,r\right)&=&2\,r^2 \end{matrix}$ In this form it is easy to find all the solutions. Factor $2 r 2$ . Then $(x - 2 r)$ can take on all integer values below $\sqrt{2}r$ . Since the problem is symmetric in $x$ and $y$ these values are all distinct pairs not counting order for the lengths of the legs of the triangle.

In the specific case with $r = 3$ the factors of 18 below $\sqrt{2}r$ are just 1,2,3. Therefore, there will be 3 values for $(x, y, z)$ : (7,24,25), (8,15,7), (9,12,15). Polytope noted that there are always 3 solutions for any prime $r$ > 2.

Retrieved from "http://www.efnet-math.org/w/Solnov1405"