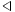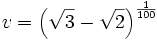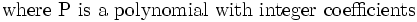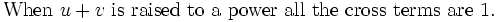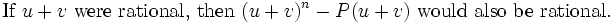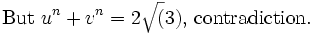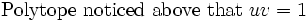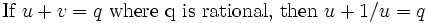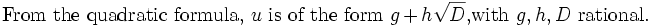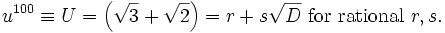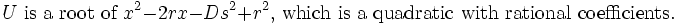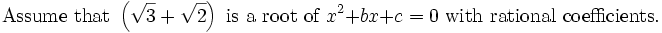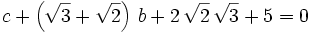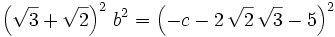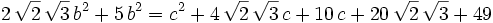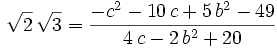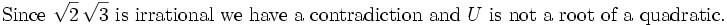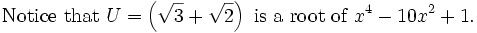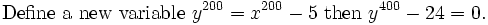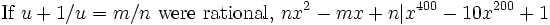Solnov2105

Solution from Polytope:

$\mbox{Let }u=\left(\sqrt{3}+\sqrt{2}\right)^{{{1}\over{100}}}\,$

$v=\left(\sqrt{3}-\sqrt{2}\right)^{{{1}\over{100}}}\,$

$\mbox{notice that }uv = 1\,$

$\mbox{You can show that }(u+v)^n = u^n + v^n + P(u+v),\,$

$\mbox{where P is a polynomial with integer coefficients}\,$

$\mbox{When }u+v\mbox{ is raised to a power all the cross terms are 1.}\,$

$\mbox{If }u+v\mbox{ were rational, then }(u+v)^n - P(u+v)\mbox{ would also be rational.}\,$

$\mbox{But }u^n + v^n = 2 \sqrt(3)\mbox{, contradiction.}\,$

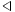
$\triangleleft$

Solution from ramanujan and landen:

$\mbox{Polytope noticed above that }uv = 1\,$

$\mbox{If }u+v=q\mbox{ where q is rational, then }u+1/u=q\,$

$\mbox{From the quadratic formula, }u\mbox{ is of the form }g + h\sqrt{D}\mbox{,with }g,h,D\mbox{ rational.}$

$u^{100}\equiv U =\left(\sqrt{3}+\sqrt{2}\right)=r+s\sqrt{D}\mbox{ for rational }r,s.\,$

$U\mbox{ is a root of }x^2-2rx-Ds^2+r^2\mbox{, which is a quadratic with rational coefficients.}\,$

$\mbox{Assume that }\left(\sqrt{3}+\sqrt{2}\right)\mbox{ is a root of }x^2 + bx + c=0\mbox{ with rational coefficients.}$

$\mbox{Substitute }\left(\sqrt{3}+\sqrt{2}\right)\mbox{ into }x^2 + bx + c=0$

$c+\left(\sqrt{3}+\sqrt{2}\right)\,b+2\,\sqrt{2}\,\sqrt{3}+5=0$

$\left(\sqrt{3}+\sqrt{2}\right)\,b=-c-2\,\sqrt{2}\,\sqrt{3}-5\,$

$\left(\sqrt{3}+\sqrt{2}\right)^2\,b^2=\left(-c-2\,\sqrt{2}\,\sqrt{3 }-5\right)^2$

$2\,\sqrt{2}\,\sqrt{3}\,b^2+5\,b^2=c^2+4\,\sqrt{2}\,\sqrt{3}\,c+10\, c+20\,\sqrt{2}\,\sqrt{3}+49$

$\sqrt{2}\,\sqrt{3}={{-c^2-10\,c+5\,b^2-49}\over{4\,c-2\,b^2+20}}$

$\mbox{Since }\sqrt{2}\,\sqrt{3}\mbox{ is irrational we have a contradiction and }U\mbox{ is not a root of a quadratic.}$

$\mbox{Then }u\mbox{ is also not a root of a quadratic, which is a contradiction.}\,$

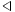
$\triangleleft$

Another proof by landen

$\mbox{Notice that }U=\left(\sqrt{3}+\sqrt{2}\right)\mbox{ is a root of }x^4-10x^2 + 1.$

The way to "notice" this is to get Pari (http://pari.math.u-bordeaux.fr) to suggest it and Maxima (http://maxima.sourceforge.net) to verify it symbolically.

$\mbox{Then }u = U^{\frac{1}{100}}\mbox{ is a root of }x^{400}-10x^{200}+1.$

$\mbox{Define a new variable }y^{200}=x^{200}-5\mbox{ then }y^{400} - 24 = 0.\,$

Since 3|24 and 3^2 does not, the polynomial in $y$ and therefore in $x$ is irreducible by the criterion of Eisenstein (http://mathworld.wolfram.com/EisensteinsIrreducibilityCriterion.html).

$\mbox{If }u+1/u =m/n\mbox{ were rational, }nx^2-mx+n | x^{400}-10x^{200}+1\,$

This is a contradiction and the proposition is established. $\triangleleft$

Retrieved from "http://www.efnet-math.org/w/Solnov2105"