Solution, January 18, 2007

Find the limit 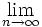$\lim_{n\rightarrow \infty}$ $\frac{1\cdot 3 \cdot 5 \cdots 2n-1}{2\cdot 4 \cdot 6 \cdots 2n}$

Honours Pre-Calc III solutions by landen

Solution I Using a famous result

After messing around it seems to work best to consider the reciprocal of the expression.

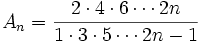
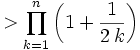
$A_n = \frac{2\cdot 4 \cdot 6 \cdots 2n }{1\cdot 3 \cdot 5 \cdots 2n-1}$ $= \prod_{k=1}^{n}\left(1+\frac{1}{2\,k-1}\right)$ $> \prod_{k=1}^{n}\left(1+\frac{1}{2\,k}\right)$

If we expand the product on the right we get:

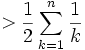
$A_n > 1 + \sum_{k=1}^{n}\frac{1}{2\,k} + \mbox{complicated positive stuff}$ $>\frac{1}{2}\sum_{k=1}^{n}\frac{1}{k}$

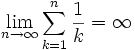$\lim_{n\rightarrow \infty} \sum_{k=1}^{n}\frac{1}{k} = \infty$ This is the famous harmonic sum limit. (http://en.wikipedia.org/wiki/Harmonic_series_(mathematics)) It is also probably in your book.

This establishes that the original expression goes to zero.
$\square$

Solution II Using a lucky guess of something to prove but no outside theorems

Proof by induction that: 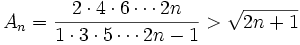$A_n = \frac{2\cdot 4 \cdot 6 \cdots 2n }{1\cdot 3 \cdot 5 \cdots 2n-1} > \sqrt{2n+1}$

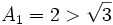$A_1 = 2 > \sqrt{3}$ So the base case is true. Now the induction case.

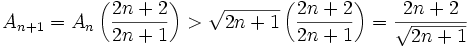
$A_{n+1} = A_n \left(\frac {2n+2}{2n+1}\right) > \sqrt{2n+1}\left(\frac {2n+2}{2n+1}\right)=\frac {2n+2}{\sqrt{2n+1}}$

Now we drop back and prove a little result to use:

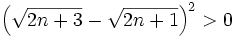$\left(\sqrt{2n+3}-\sqrt{2n+1}\right)^2 > 0$ expanding this:

$2n+2 > \sqrt{2n+3}\,\sqrt{2n+1}$

$A_{n+1}> \frac {2n+2}{\sqrt{2n+1}} > \frac{\sqrt{2n+3}\,\sqrt{2n+1}}{\sqrt{2n+1}} = \sqrt{2n+3}$

So by induction 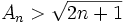$A_n > \sqrt{2n+1}$ and goes to $\infty$ as $n\,$ does. Again our original limit is 0.
$\square$

Retrieved from "http://www.efnet-math.org/w/Solution%2C_January_18%2C_2007"