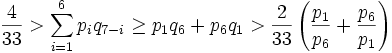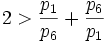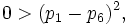Solution 1 May 29, 2007

Problem

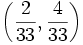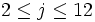Does there exist two unfair 6-sided dice labeled with numbers 1..6 each such that probability of their sum being j is a number in $\left(\frac2{33},\frac4{33}\right)$ for each $2\leq j\leq 12$ ?

Solution

This is impossible. Let the probabilities for the sides of the first die be $p_1,\, p_2,\ldots,\, p_6$ and similarily let $q_1,\ldots,\,q_6$ be those for the second die.

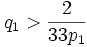The probability for the dice showing a sum of 2 is $p_1q_1>\frac2{33}$ . This implies $q_1>\frac2{33p_1}$ . Similarily, 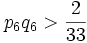$p_6q_6>\frac2{33}$ is the probability of a sum of 12, and we have $q_6>\frac2{33p_6}$ . For the probability of a sum of 7 we have

$\frac4{33}>\sum_{i=1}^6p_iq_{7-i} \geq p_1q_6+p_6q_1>\frac2{33}\left(\frac{p_1}{p_6}+\frac{p_6}{p_1}\right)$

$2 > \frac{p_1}{p_6}+\frac{p_6}{p_1}$

This is a contradiction; multiplying both sides by 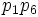$p_1p_6\,$ and bringing all terms to one side gives

$0 > (p_1-p_6)^2,\,$

which is false. This completes the proof.

Retrieved from "https://www.efnet-math.org:443/w/Solution_1_May_29%2C_2007"