Solution 1 Tues., Dec. 19, 2006

1. Find: 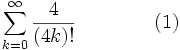$\sum_{k=0}^\infty \frac{4}{(4k)!}\qquad\qquad(1)$

Analysis

Define 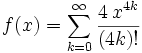$f(x)=\sum_{k=0}^\infty \frac{4\,x^{4k}}{(4k)!}$

Next, notice that 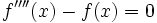$f^{\prime\prime\prime\prime}(x) -f(x)=0$

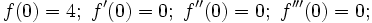$f(0)=4;\ f^{\prime}(0)=0;\ f^{\prime\prime}(0)=0;\ f^{\prime\prime\prime}(0)=0;$ The characteristic equation for this ODE is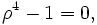 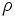$\rho^4-1=0,\,$ $\rho\,$ can be: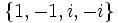 $\{1,-1,i,-i\}\,$

This differential equation has the solution: 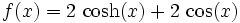$f(x)=2\,\cosh(x)+2\,\cos(x)$

Then 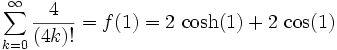$\sum_{k=0}^\infty \frac{4}{(4k)!} = f(1) = 2\,\cosh(1)+2\,\cos(1)$

Numerically this is 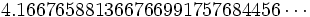$4.166765881366766991757684456\cdots$ which is the same as the sum of the first 11 terms of (1).

$\square\,$

Retrieved from "http://www.efnet-math.org/w/Solution_1_Tues.%2C_Dec._19%2C_2006"