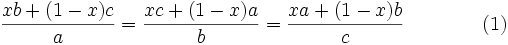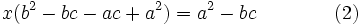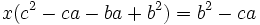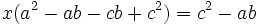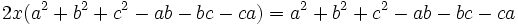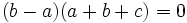Solution 28 Dec 2006
If 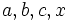 are real numbers such that
are real numbers such that 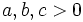 and
and
then prove that  .
.
Proof. Assume that 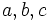 are not all equal.
are not all equal.
Note that equation (1) has a cyclic symmetry, i.e. it is unchanged if we replace 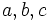 by
by 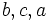 (or
(or  ) respectively.
) respectively.
Take the first two terms of (1) and multiply by 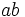 , then isolate
, then isolate  :
:
Likewise, by cyclic symmetry, we have
Adding these three equations yields
By the rearrangement inequality, we have that 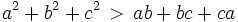 (this uses that
(this uses that 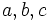 are not all equal), so
are not all equal), so 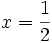 .
.
Then (2) becomes
But 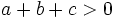 because
because 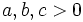 , so this implies
, so this implies 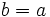 . By symmetry this implies
. By symmetry this implies  , contradicting the assumption.
, contradicting the assumption.