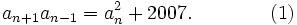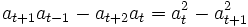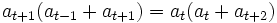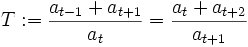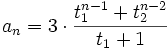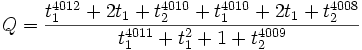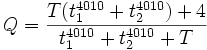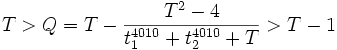Solution April 10, 2007
Problem
Let a sequence be defined as follows: a1 = 3, a2 = 3, and for 
Find the largest integer less than or equal to 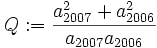 .
.
Solution
Take the difference of (1) for 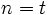 and
and 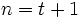 .
.
By induction we see that 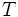 is independent of
is independent of 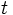 ,
so, perhaps surprisingly,
,
so, perhaps surprisingly, 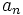 is generated by the linear recurrence
is generated by the linear recurrence
 .
.
In our case, 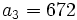 and
and 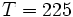 . The characteristic equation of (2),
. The characteristic equation of (2), 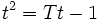 has solutions
has solutions
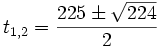 with
with 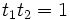 and
and 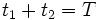 , and we get a closed form
solution for
, and we get a closed form
solution for 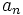 , namely
, namely
Then,
The inequalities follow easily from 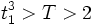 .
.
Thus, 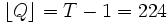 which answers the problem.
which answers the problem.