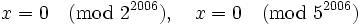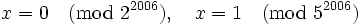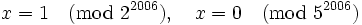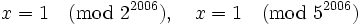Solution April 12, 2007
Problem
Find the number of positive integers x < 102006 such that x2 − x is divisible by 102006.
Solution
Note that 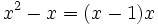 and
and 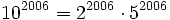 .
.
Because 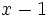 and
and 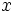 are coprime, exactly one
of them must be divisibly by
are coprime, exactly one
of them must be divisibly by 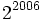 and likewise, one of them
must be divisible by
and likewise, one of them
must be divisible by 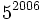 . This gives us four cases:
. This gives us four cases:
By the Chinese Remainder Theorem (http://en.wikipedia.org/wiki/Chinese_remainder_theorem), each of these cases has a unique solution 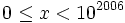 .
.
One of these four solutions is 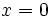 which is not positive. This leaves us with 3 solutions which satisfy all required conditions.
which is not positive. This leaves us with 3 solutions which satisfy all required conditions.