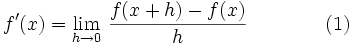Solution Dec. 8, 2006
Let 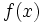 be a function of a real variable with real values.
be a function of a real variable with real values.
If  is irrational then
is irrational then 
If  is rational
is rational  in lowest terms,
in lowest terms, 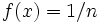
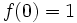
Show that 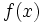 is nowhere differentiable.
is nowhere differentiable.
Proof:
If 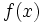 is differentiable then its derivative at
is differentiable then its derivative at  is given by this limit:
is given by this limit:
Suppose  is rational. Take a sequence of irrational numbers that converges to 0, e.g.,
is rational. Take a sequence of irrational numbers that converges to 0, e.g., 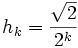
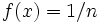 for some integer
for some integer  since
since  is rational.
is rational.
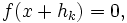 since
since 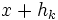 is irrational.
is irrational.
Using these values in (1) we get:
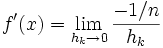 Which does not exist.
Which does not exist.
Now consider  is irrational.
is irrational.
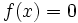
As we take the limit in (1), anytime h is rational the quotient is 0. So if the derivative exists it is 0.
 will have an infinite sequence of rational decimals which converges to it, e.g., for
will have an infinite sequence of rational decimals which converges to it, e.g., for 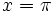 we have:
we have: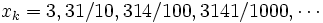
Define:  and apply this to (1)
and apply this to (1)
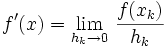
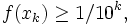 cancellation to lowest terms can only make the denominator smaller.
cancellation to lowest terms can only make the denominator smaller.
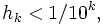 so we have:
so we have:
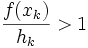
All these large values for the quotient are in between values of 0 mentioned above. Therefore the limit does not exist.