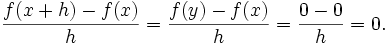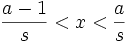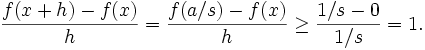Solution Dec. 8, 2006 2

Here's a slightly different solution, but both proofs rely on the fact that between any two distinct numbers, there are both rational and irrational numbers.

First, suppose $x$ is rational. Then $x = m / n$ and $f (x) = 1 / n$ for integers $m, n$ . (Notice that $0 = 0 / 1$ , so this is true for all rationals.) Rather than consider the difference quotient here, we'll instead notice that for any $δ > 0$ , there's an irrational number $y$ with $| x - y | < δ$ . But $f (y) = 0$ , so $| f (x) - f (y) | = 1 / n > 0$ . This means $f$ is not continuous at $x$ , and therefore can't be differentiable there.

Suppose now that $x$ is irrational, so $f (x) = 0$ . Let $δ > 0$ be given. Then there must be an irrational $y$ with $0 < | y - x | < δ$ . Letting $h = y - x$ , we have $| h | < δ$ , and

$\frac{f(x+h) - f(x)}{h} = \frac{f(y)-f(x)}{h} = \frac{0-0}{h} = 0.$

Since $δ$ was an arbitrary positive number, this means that if $f'(x)$ exists, it must be 0.

Now, let $q$ be a rational number with $x < q < x + δ$ , so $q = r / s$ for integers $r, s$ . Since $x$ is irrational, it has to lie between two consecutive rationals with denominator $s$ , i.e.

$\frac{a-1}{s} < x < \frac{a}{s}$

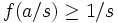for some integer $a$ , and since $q = r / s > x$ , this means that $a/s \le q < x + \delta$ . While we don't know if $a$ and $s$ share any common factors, we do know that $f(a/s) \ge 1/s$ , since dividing out the factors decreases the denominator. Now, let $h = a / s - x$ , so $0 < h < δ$ . In fact, we even have $h < 1 / s$ . Plugging this into the difference quotient gives us

$\frac{f(x+h)-f(x)}{h} = \frac{f(a/s) - f(x)}{h} \ge \frac{1/s - 0}{1/s} = 1.$

Therefore, if $f'(x)$ exists, it must be at least 1, a contradiction.

Therefore, $f$ is differentiable nowhere.

Retrieved from "http://www.efnet-math.org/w/Solution_Dec._8%2C_2006_2"