Solution Feb 12, 2012
Problem
Suppose X is a finite set such that | X | = 2k for some positive integer k. Suppose there's a family F of subsets of X, where each element of F has cardinality k, and such that every subset of X having cardinality k − 1 is uniquely contained in some element of F. Prove that k + 1 is prime.
Solution
Without loss of generality let 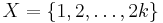 . For
. For 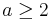 , I claim that the number of sets in F containing
, I claim that the number of sets in F containing 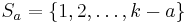 is precisely
is precisely 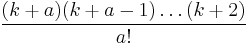 .
.
There are 2k − (k − a) = k + a numbers in X − Sa. Choosing any a − 1 numbers in X − Sa and including them in Sa will provide us with a subset of cardinality k − 1, which, by the condition on F, is uniquely contained in some set in F. There are clearly a! repetitions in creating a set in this manner, so the claim is proved.
Since 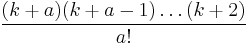 is integer for all
is integer for all 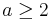 , it's now easy to see that k + 1 is prime.
, it's now easy to see that k + 1 is prime.