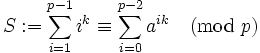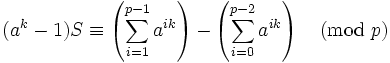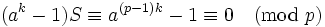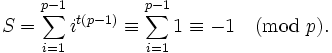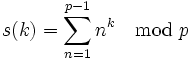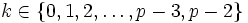Solution February 13, 2007

Solution I from int-e

Let 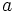$a\,$ be a primitive root (http://en.wikipedia.org/wiki/Primitive_root_modulo_n) modulo 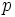$p\,$ . Then, 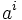$a^i\,$ covers every non-zero remainder modulo 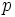$p\,$ exactly once for $i = 0\ldots p-2\,$ , so

$S := \sum_{i=1}^{p-1}i^k\equiv \sum_{i=0}^{p-2}a^{ik}\pmod p$

Therefore,

$(a^k-1)S \equiv \left(\sum_{i=1}^{p-1}a^{ik}\right) - \left(\sum_{i=0}^{p-2}a^{ik}\right)\pmod{p}$

$(a^k-1)S \equiv a^{(p-1)k} - 1 \equiv 0 \pmod p$

by Fermat's little theorem (http://en.wikipedia.org/wiki/Fermat's_little_theorem).

If 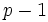$p-1\,$ does not divide 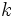$k\,$ , then 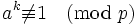$a^k\not\equiv 1 \pmod{p}\,$ , so we can divide by 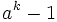$a^k-1\,$ and obtain

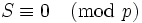$S \equiv 0 \pmod p\,$ .

If 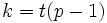$k = t(p-1)\,$ , we can evaluate 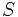$S\,$ directly using Fermat's little theorem again:

$S = \sum_{i=1}^{p-1}i^{t(p-1)} \equiv \sum_{i=1}^{p-1}1 \equiv -1\pmod p.$

This covers all cases. $\square$

Solution II from landen

For 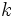$k\,$ a positive integer and 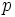$p\,$ a prime, what are the possible values of:

$s(k)=\sum_{n=1}^{p-1}n^k \mod{p}$

From Fermat's little theorem (http://en.wikipedia.org/wiki/Fermat's_little_theorem) it is sufficient to reduce 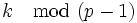$k \mod {(p-1)}\,$ to give only a finite number of values for each prime.

$k\in \left\{0,1,2,\dots,p-3,p-2\right\}\,$

Exploring with some famous sums:
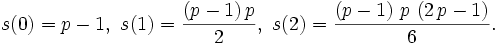
$s(0)=p-1,\ s(1)=\frac{(p-1)\,p}{2},\ s(2)={{\left(p-1\right)\,p\,\left(2\,p-1\right)}\over{6}}.$

The 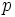$p\,$ factors suggest that for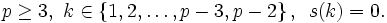 $p\geq 3,\ k\in \left\{1,2,\dots,p-3,p-2\right\},\,\ s(k)=0.$

We can prove this by induction on 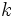$k\,$ and stopping at 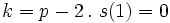$k=p-2\,. \ s(1)=0$ so the base case is easy.

Consider:
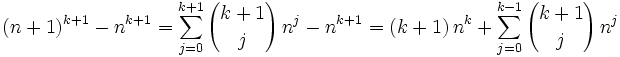
$(n+1)^{k+1}-n^{k+1}=\sum_{j=0}^{k+1}{{k+1\choose j}\,n^{j}}-n^{k+1} =(k+1)\,n^k + \sum_{j=0}^{k-1}{{k+1\choose j}\,n^{j}}$

Summing both sides of this equation from 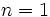$n=1\,$ to $n=p-1:\,$
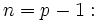
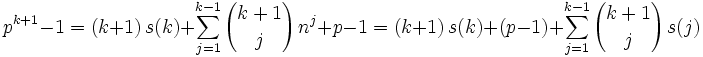
$p^{k+1}-1 = (k+1)\,s(k) + \sum_{j=1}^{k-1}{{k+1\choose j}\,n^{j}}+p-1=(k+1)\,s(k) + (p-1)+\sum_{j=1}^{k-1}{{k+1\choose j}\,s(j)}$

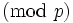The left side of the equation had all middle terms cancel. If we now assume $s(j)=0,\ j\in \left\{1,2,\dots,k-2,k-1\right\},\,$ by induction hypothesis then $(\mathrm{mod}\ p)$ :
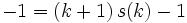
$-1=(k+1)\,s(k)-1\,$
$s(k)=0\,$
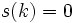
The final conclusion is valid because $k+1 \neq 0 \mod p$ .

$\square$

Retrieved from "http://www.efnet-math.org/w/Solution_February_13%2C_2007"