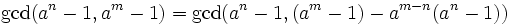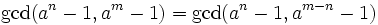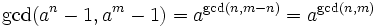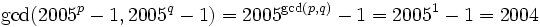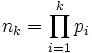Solution February 21, 2007

Problem

Show that there exist infinitely many square-free positive integers n that divide $2005 n - 1$ .

Solution

Note: The proof that follows uses some basic facts about the greatest common divisor (http://en.wikipedia.org/wiki/Greatest_Common_Divisor).

Lemma: for positive integers $a, n$ and $m$ ,

$\gcd(a^n-1, a^m-1) = a^{\gcd(n,m)}-1\quad\quad(1)$

Proof: Assume (1) is wrong. Then there is a counterexample $(a, n, m)$ that minimizes $n + m$ . If $n = m$ then (1) is true because $g c d (x, x) = x$ for all $x$ , so 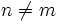$n\neq m$ . Without loss of generality, we can assume $n < m$ . But then

$\gcd(a^n-1, a^m-1) = \gcd(a^n-1, (a^m-1) - a^{m-n}(a^n-1))\,$

$\gcd(a^n-1, a^m-1) = \gcd(a^n-1, a^{m-n}-1)\,$

But $(n - m) + m < n + m$ so we can apply (1) to get

$\gcd(a^n-1, a^m-1) = a^{\gcd(n, m-n)} = a^{\gcd(n, m)}\,$

contrary to our assumption that $(a, n, m)$ is a counterexample. $\square$

In particular, if $p$ and $q$ are different primes, then

$\gcd(2005^p-1, 2005^q-1) = 2005^{\gcd(p,q)}-1 = 2005^1-1 = 2004\,$

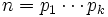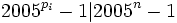Let us now turn to the problem. Consider the factorization of a solution, $n=p_1\cdots p_k$ . Note that $2005^{p_i}-1 | 2005^n-1$ .

Obviously (http://en.wikipedia.org/wiki/Fermat's_little_theorem), we can not hope for infinitely many solutions to 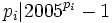$p_i|2005^{p_i}-1$ .

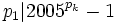However we can arrange that $p_{i+1}|2005^{p_i}-1$ and $p_1|2005^{p_k}-1$ . This solves the problem because then each prime factor of $n$ divides $2005 n - 1$ , and $n$ is square-free. We can accomplish this as follows:

Define $p 1 = 3$ , $p 2 = 13$ and 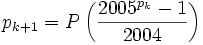$p_{k+1}=P\left(\frac{2005^{p_k}-1}{2004}\right)$ for $k > 1$ , where $P (n)$ denotes the smallest prime divisor of $n$ .

Claim: This defines a sequence of distinct primes such that $p_{i+1}|2005^{p_i}-1$ .

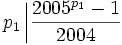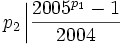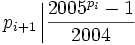Proof: A quick calculation shows that $p_1\left|\frac{2005^{p_1}-1}{2004}\right.$ and $p_2\left|\frac{2005^{p_1}-1}{2004}\right.$ . For $i > 1$ , $p_{i+1}\left|\frac{2005^{p_i}-1}{2004}\right.$ is true by construction.

In order to show that the primes are distinct, assume that $p i = p j$ for some minimal $i < j$ .

If $i = 1$ and $j = 2$ , then $p_i\neq p_j$ by definition.
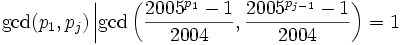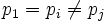
If $i = 1$ and $j > 2$ then $p_1\neq p_{j-1}$ because $j$ was chosen to be minimal, so that $\gcd(p_1,p_j)\left|\gcd\left(\frac{2005^{p_1}-1}{2004}, \frac{2005^{p_{j-1}}-1}{2004}\right)=1\right.$ , so $p_1=p_i\neq p_j$
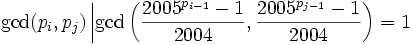If $i > 1$ then $p_{i-1}\neq p_{j-1}$ , by minimality of $i$ and $j$ , and $\gcd(p_i,p_j)\left|\gcd\left(\frac{2005^{p_{i-1}}-1}{2004}, \frac{2005^{p_{j-1}}-1}{2004}\right)=1\right.$ so $p_i\neq p_j$ again.

We have a contradiction in each case, proving our claim. $\square$

It is also true that 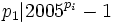$p_1|2005^{p_i}-1$ for all $i$ so we can define the infinite sequence of distinct square-free numbers

$n_k = \prod_{i=1}^k p_i$

that all satisfy 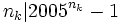$n_k|2005^{n_k}-1$ . This completes the solution.

$\square$

Retrieved from "http://www.efnet-math.org/w/Solution_February_21%2C_2007"