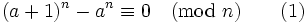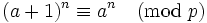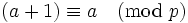Solution February 22, 2007

Problem

Find all positive integer pairs $(a, n)$ such that 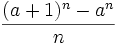$\frac{(a+1)^n-a^n}{n}$ is an integer.

Solution

In other words, find all positive integer pairs $(a, n)$ such that

$(a+1)^n - a^n \equiv 0 \pmod n\quad\quad(1)$

(1) is obviously satisfied if $n = 1$ . We will show that the pairs $(a,1)$ are the only solutions to the problem.

Assume to the contrary that we have a solution of (1), $(a, n)$ , with $n > 1$ . Then $n$ has a smallest prime divisor $p$ .

All prime divisors of $p - 1$ are smaller than $p$ , so we have $gcd(n, p - 1) = 1$ . By Bézout's identity (http://en.wikipedia.org/wiki/B%C3%A9zout%27s_identity) there are integers $b$ and $c$ such that

$bn + c(p-1) = 1\,$ .

Consider (1) modulo $p$ (remember that $p$ divides $n$ ),

$(a+1)^n \equiv a^n\pmod p\,$

and raise both sides to the $b$ -th power:

$(a+1)^{bn} \equiv (a+1)^{1-c(p-1)} \equiv a^{1-c(p-1)} \equiv a^{bn}\pmod p\,$

By repeated application of Fermat's little theorem (http://en.wikipedia.org/wiki/Fermats_little_theorem) - each application reduces $| c |$ by $1$ - this is equivalent to

$(a+1) \equiv a \pmod p\,$

which is a contradiction because $p > 1$ .

$\square$

Retrieved from "http://www.efnet-math.org/w/Solution_February_22%2C_2007"