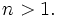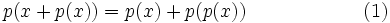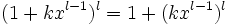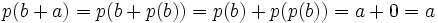Solution January 31 2007
Problem
Find all real polynomials such that
Solution I by int_e
Note that if a polynomial equation (i.e. an equation with polynomials in  on both sides) is true for infinitely many real numbers, it is
satisfied for all complex numbers. To see why, consider the difference
of the two sides as a polynomial in
on both sides) is true for infinitely many real numbers, it is
satisfied for all complex numbers. To see why, consider the difference
of the two sides as a polynomial in  over the complex numbers. For real
over the complex numbers. For real  ,
the polynomial evaluates to the same value over the complex numbers as
over the real numbers, so it has infinitely many zeros over the complex
numbers. It follows that it is the zero polynomial, and the equation is
satisfied for all complex numbers, as claimed. So we will solve the
problem for complex polynomials first, and then restrict the solutions
to the real polynomials.
,
the polynomial evaluates to the same value over the complex numbers as
over the real numbers, so it has infinitely many zeros over the complex
numbers. It follows that it is the zero polynomial, and the equation is
satisfied for all complex numbers, as claimed. So we will solve the
problem for complex polynomials first, and then restrict the solutions
to the real polynomials.
We will consider a few cases.
- If
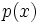 is a constant polynomial,
is a constant polynomial,  , then
, then  , i.e.
, i.e. 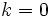 and
and  . This is a solution of the problem.
. This is a solution of the problem.
- Otherwise, if all zeros of
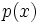 are
are 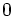 , i.e.
, i.e. 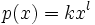 with
with 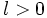 and
and 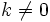 , then
, then
- The left side has
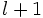 non-zero terms after expanding, while the right side has
non-zero terms after expanding, while the right side has 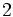 . By comparing coefficients we see that these two numbers must equal. It is easily verified that
. By comparing coefficients we see that these two numbers must equal. It is easily verified that 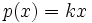 is indeed a solution of the problem for all
is indeed a solution of the problem for all  .
.
- In all other cases,
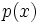 has a zero
has a zero 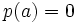 with
with 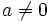 , by the fundamental theorem of algebra. (http://en.wikipedia.org/wiki/Fundamental_theorem_of_algebra) Likewise, there's a root
, by the fundamental theorem of algebra. (http://en.wikipedia.org/wiki/Fundamental_theorem_of_algebra) Likewise, there's a root 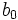 of
of 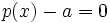 .
.
- Now if
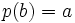 then by (1),
then by (1),
-
- By induction it follows that
 for all natural numbers
for all natural numbers  . Thus,
. Thus, 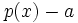 has infinitely many zeros and must be constant. This means that
has infinitely many zeros and must be constant. This means that 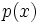 is constant as well, contrary to our assumptions.
is constant as well, contrary to our assumptions. 
In summary, the solutions are the polynomials 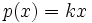 with
with 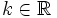 . (Note that this includes the first case)
. (Note that this includes the first case)
Solution II by landen
Find all real polynomials such that
By direct substitution we get that 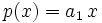 is a solution for any real
is a solution for any real 
Let 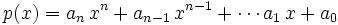 with
with
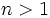 and
and 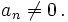
Letting 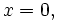 we have
we have 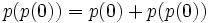 and
and 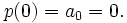
For simpler notation take 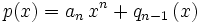 where
where 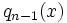 is a polynomial of lower degree than
is a polynomial of lower degree than 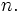
By expansion of the left side of (1) we get.
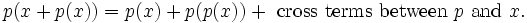
The cross term of highest degree must have a least one  to be a cross term and then as many powers of
to be a cross term and then as many powers of 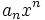 as possible. Any powers of
as possible. Any powers of 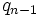 will give smaller cross terms.
will give smaller cross terms.
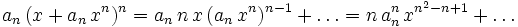 using the binomial theorem.
using the binomial theorem.
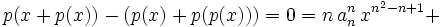 lower order cross terms.
lower order cross terms.
 which violates our assumption that it was nonzero for some
which violates our assumption that it was nonzero for some 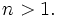 Therefore, there are no solutions of degree
Therefore, there are no solutions of degree