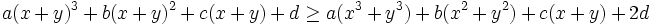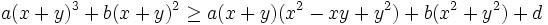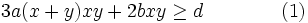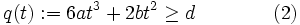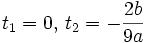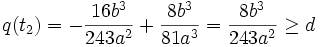Solution June 02, 2007
Problem
Find all polynomials of degree 3, such that for each 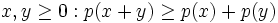
Solution
Let
-
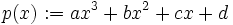 .
.
For all 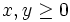 we have
we have
First let x = y = 0 to see that 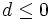 .
.
Now set x = y and let x go to infinity we see from (1) that 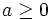 .
.
Consider the inequality
(2) follows from (1) for all 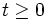 by letting
by letting 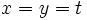 . On the other hand, if we let
. On the other hand, if we let 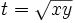 then (1) follows from (2) and the arithmetic-geometric mean
inequality,
then (1) follows from (2) and the arithmetic-geometric mean
inequality, 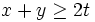 .
.
If 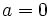 , we find that
, we find that 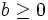 by letting t go to infinity, and this suffices to satisfy (2).
by letting t go to infinity, and this suffices to satisfy (2).
Assume that 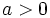 . We want to find a condition on d such that (2) is always satisfied. We start by minimizing q(t) for
. We want to find a condition on d such that (2) is always satisfied. We start by minimizing q(t) for 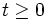 , so we set its derivative to 0:
, so we set its derivative to 0:
Note that 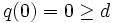 so only minima greater than 0 need to be considered.
so only minima greater than 0 need to be considered.
If 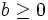 , then
, then 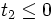 , so there are no other minima to consider.
, so there are no other minima to consider.
If 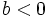 , then
, then
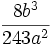 is negative in this case, so this is a stronger condition on d than we already had.
is negative in this case, so this is a stronger condition on d than we already had.
In summary, p(x) is a polynomial satisfying 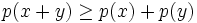 for all
for all 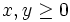 in the following cases:
in the following cases:
-
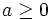 ,
, 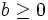 and
and 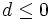
-
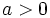 ,
, 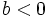 and
and 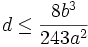
No other possibilities for p(x) exist.