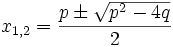Solution June 28, 2007
| Table of contents |
Problem 1
Find all positive integers 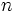 such that
such that 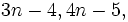 and
and 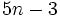 are all prime numbers.
are all prime numbers.
Solution 1
Remember that 2 is the only even prime. We consider two cases.
- n even: Then 3n − 4 is an even prime so that 3n − 4 = 2 and n = 2. The resulting numbers 2,3,7 are indeed prime so this is a solution.
- n odd: Then 5n − 3 is an even prime, and 5n − 3 = 2. This implies n = 1 which isn't a solution because 3 − 4 = − 1 is not a prime number.
So n = 2 is the only solution to the problem.
Problem 2
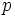 and
and 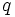 are prime numbers.
are prime numbers. 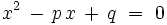 has distinct rational roots. Find all
has distinct rational roots. Find all  and
and 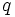 which work.
which work.
Solution 2
We can write x2 − px + q = (x − a)(x − b) where a and b are the roots of the polynomial.
By the rational roots theorem (http://en.wikipedia.org/wiki/Rational_root_theorem) (if this is too scary, see the note below), the roots of x2 − px + q = 0 are integers that divide q.
The product of the two roots must be q so we have a = − 1,b = − q or a = 1,b = q.
The sum of the two roots is equal to p which rules out the first possibility, because p > 0.
Now we have p = q + 1 where p and q are both prime. The only possibility for that is p = 3 and q = 2. That answers the problem.
Note: Instead of using the rational roots theorem, we can have a closer look at the quadratic formula. The roots of x2 − px + q are
They are only rational when p2 − 4q is a perfect square. If p is even then p2 − 4q is even and so is its square root. Similarily, if p is odd then p2 − 4q is odd and its square root is odd. In either case, 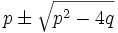 are even, so the roots are integers if they are rational.
are even, so the roots are integers if they are rational.