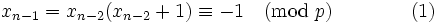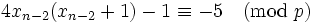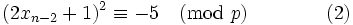Solution March 01, 2007
Problem
For all integers 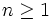 we define
we define 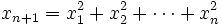 , where x1 is a positive integer. Find the least x1 such that 2006 divides x2006.
, where x1 is a positive integer. Find the least x1 such that 2006 divides x2006.
Solution
Clearly, 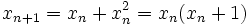 .
.
If 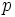 divides
divides 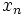 it will also divide
it will also divide 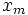 for all
for all 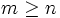 .
.
Note that 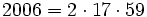 , so we can consider the sequence modulo each of these three primes separately.
, so we can consider the sequence modulo each of these three primes separately.
Assume that  .
.
Let 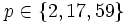 , and let
, and let  be the smallest index such that
be the smallest index such that 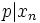 . If
. If 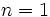 then
then 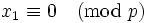 . Otherwise
. Otherwise
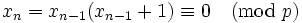 , i.e.
, i.e. 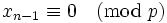 or
or 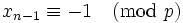 . The first possibility is ruled out by our choice of
. The first possibility is ruled out by our choice of  . If
. If 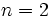 this implies
this implies 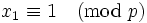 .
.
Now assume that 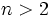 . Then,
. Then,
Now consider each 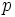 in turn.
in turn.
- If
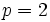 , (1) is a contradiction because
, (1) is a contradiction because  is always even.
is always even.
- If
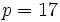 we can raise both sides of (2) to the 8-th power and use Fermat's little theorem (http://en.wikipedia.org/wiki/Fermat%27s_little_theorem). The result is
we can raise both sides of (2) to the 8-th power and use Fermat's little theorem (http://en.wikipedia.org/wiki/Fermat%27s_little_theorem). The result is 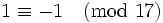 , a contradiction.
, a contradiction.
- The case
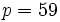 is very similar. This time, we raise both sides of (2) to the 29-th power and get
is very similar. This time, we raise both sides of (2) to the 29-th power and get 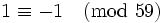 , again a contradiction.
, again a contradiction.
Note: The last two cases show that 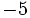 is not a quadratic residue (http://en.wikipedia.org/wiki/Quadratic_residue) modulo
is not a quadratic residue (http://en.wikipedia.org/wiki/Quadratic_residue) modulo  or
or 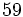 .
.
In summary, we have that 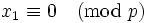 or
or 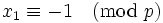 for
for  . For
. For 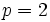 this is no restriction. So we have four cases, which we can solve using the Chinese Remainder Theorem (http://en.wikipedia.org/wiki/Chinese_remainder_theorem)
this is no restriction. So we have four cases, which we can solve using the Chinese Remainder Theorem (http://en.wikipedia.org/wiki/Chinese_remainder_theorem)
-
 and
and 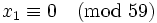 has solutions
has solutions  .
.
-
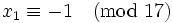 and
and 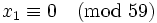 has solutions
has solutions 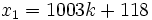 .
.
-
 and
and 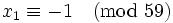 has solutions
has solutions 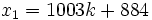 .
.
-
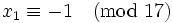 and
and 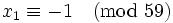 has solutions
has solutions 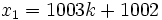 .
.
The smallest positive solution is  .
.