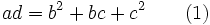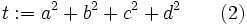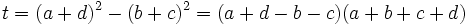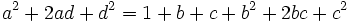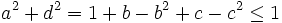Solution March 18, 2007

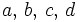$a,\,b,\,c,\,d$ are positive integers and

$ad=b^{2}+bc+c^{2}\qquad(1)$

Prove that

$t := a^{2}+b^{2}+c^{2}+d^{2}\qquad(2)$

is a composite number.

Obviously, 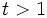$t>1\,$ . Assume that 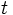$t\,$ is prime.

We can subtract (1) twice from (2) and obtain

$t = (a+d)^2 - (b+c)^2 = (a+d-b-c)(a+b+c+d)\,$

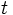For $t\,$ to be prime, we must have 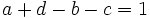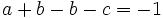$a+d-b-c = 1\,$ . ( $a+b-b-c=-1\,$ is impossible because then 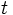$t\,$ would be negative.)

So 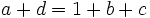$a+d = 1+b+c\,$ . Squaring both sides we get

$a^2+2ad+d^2 = 1+b+c+b^2+2bc+c^2\,$

Now subtract (1) twice to obtain

$a^2+d^2 = 1+b-b^2 +c-c^2 \leq 1$

which is a contradition. $\square$