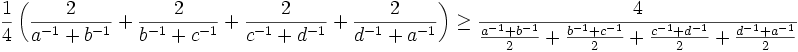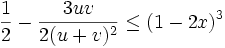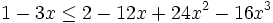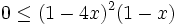Solution March 20, 2007
Problem
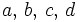 are positive real numbers satisfying the following condition:
are positive real numbers satisfying the following condition:
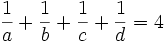
Prove that:
![\sqrt[3]{\frac{a^{3}+b^{3}}{2}}+\sqrt[3]{\frac{b^{3}+c^{3}}{2}}+\sqrt[3]{\frac{c^{3}+d^{3}}{2}}+\sqrt[3]{\frac{d^{3}+a^{3}}{2}}\leq 2(a+b+c+d)-4](https://efnet-math.org/wiki/images/math/6144b79e3966e6709ec6330b2b4acfb3.png)
Solution
For brevity, define
We will show that
whenever  .
.
Lemma: (1) is true for all  if and only if
if and only if
holds for all 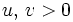
Proof: It's easy to see that (2) follows from (1): just set 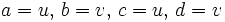 .
.
So assume that (2) is true for all 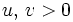 and let
and let  . Sum (2) for
. Sum (2) for 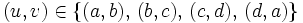 . We obtain
. We obtain
Now by the arithmetic-harmonic means inequality (http://planetmath.org/encyclopedia/ArithmeticGeometricMeansInequality.html),
and (1) follows from that and (3), completing the proof of the lemma. 
All that's left to show is (2). For this purpose, let  . It's easy to see (http://planetmath.org/encyclopedia/ArithmeticGeometricMeansInequality.html) that
. It's easy to see (http://planetmath.org/encyclopedia/ArithmeticGeometricMeansInequality.html) that 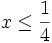 .
.
Divide (2) by 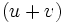 , raise it to the 3rd power and simplify:
, raise it to the 3rd power and simplify:
The latter inequality is true for all 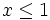 . This completes the proof of (2), and by our Lemma, proves (1).
. This completes the proof of (2), and by our Lemma, proves (1). 
![L := \sqrt[3]{\frac{a^{3}+b^{3}}{2}}+\sqrt[3]{\frac{b^{3}+c^{3}}{2}}+\sqrt[3]{\frac{c^{3}+d^{3}}{2}}+\sqrt[3]{\frac{d^{3}+a^{3}}{2}}](https://efnet-math.org/wiki/images/math/ab38b356e86ec256fd658b7bd1fb37e5.png)
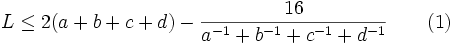
![\sqrt[3]{\frac{u^{3}+v^{3}}{2}}\leq u+v-\frac{2}{u^{-1} + v^{-1}}\qquad(2)](https://efnet-math.org/wiki/images/math/4eccb3bff3cadafce8bc44373a15e72d.png)